相關概念
函式
在數學中,疊代函式是在分形和動力系統中深入研究的對象。疊代函式是重複的與自身複合的函式,這個過程叫做疊代。
模型
算法
疊代算法是用計算機解決問題的一種基本方法。它利用計算機運算速度快、適合做重複性操作的特點,讓計算機對一組指令(或一定步驟)進行重複執行,在每次執行這組指令(或這些步驟)時,都從變數的原值推出它的一個新值。
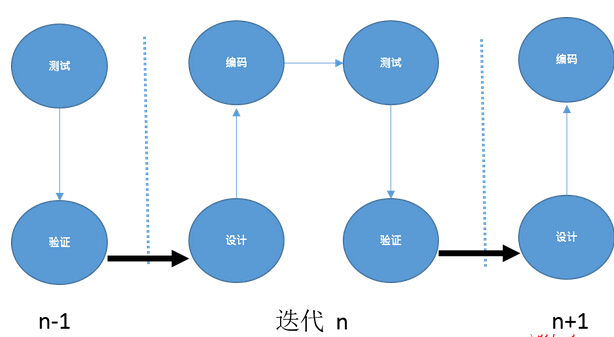
RUP模型
理解
如果認為這個解釋難以理解,可以這樣想:
我們開發一個產品,如果不太複雜,會採用
瀑布模型,簡單的說就是先定義需求,然後構建框架,然後寫代碼,然後測試,最後發布一個產品。
這樣,幾個月過去了,直到最後一天發布時,大家才能見到一個產品。
這樣的方式有明顯的缺點,假如我們對用戶的需求判斷的不是很準確時——這是很常見的問題,一點也不少見——你工作了幾個月甚至是幾年,當你把產品拿給客戶看時,客戶往往會大吃一驚,這就是我要的東西嗎?
方法
疊代的方式就有所不同,假如這個產品要求6個月交貨,我在第一個月就會拿出一個產品來,當然,這個產品會很不完善,會有很多功能還沒有添加進去,bug很多,還不穩定,但客戶看了以後,會提出更詳細的修改意見,這樣,你就知道自己距離客戶的需求有多遠,我回家以後,再花一個月,在上個月所作的
需求分析、框架設計、代碼、測試等等的基礎上,進一步改進,又拿出一個更完善的產品來,給客戶看,讓他們提意見。
就這樣,我的產品在功能上、質量上都能夠逐漸逼近客戶的要求,不會出現我花了大量心血後,直到最後發布之時才發現根本不是客戶要的東西的情況。
優勢
這樣的方法很不錯,但他也有自己的缺陷,那就是周期長、成本很高。在應付大項目、高風險項目——就比如是太空梭的控制系統時,疊代的成本比項目失敗的風險成本低得多,用這種方式明顯有優勢。
如果你是給自己的單位開發一個小MIS,自己也比較清楚需求,工期上也不過花上個把月的時間,用疊代就有點殺雞用了牛刀,那還是
瀑布模型更管用,即使是做得不對,頂多再花一個月重來,沒什麼了不起。
基本算法
在java中Iterative 僅用於遍歷集合,本身並不提供盛裝對象的能力。如果需要創建Iterative對象,則必須有一個被疊代的集合。沒有集合的Iterative仿佛無本之木,沒有存在的價值。
iterative是反覆的意思,所以,有時候,疊代也會指循環執行,反覆執行的意思。
利用疊代算法解決問題,需要做好以下三個方面的工作:
確定變數
在可以用疊代算法解決的問題中,至少存在一個直接或間接地不斷由舊值遞推出新值的變數,這個變數就是疊代變數。
建立關係式
所謂疊代關係式,指如何從變數的前一個值推出其下一個值的公式(或關係)。疊代關係式的建立是解決疊代問題的關鍵,通常可以使用
遞推或倒推的方法來完成。
過程控制
在什麼時候結束疊代過程?這是編寫疊代程式必須考慮的問題。不能讓疊代過程無休止地重複執行下去。疊代過程的控制通常可分為兩種情況:一種是所需的疊代次數是個確定的值,可以計算出來;另一種是所需的疊代次數無法確定。對於前一種情況,可以構建一個固定次數的循環來實現對疊代過程的控制;對於後一種情況,需要進一步分析出用來結束疊代過程的條件。
例1 : Fibonacci Sequence(斐波那契數列)
即這樣一個數列:0、1、1、2、3、5、8、13......,在數學上該數列定義為:
F(0)=0,F(1)=1; F(n) = F(n-1)+F(n-2) (n≥2,n∈N*)。
一般該數列可以遞歸實現,下面是用C語言 疊代 實現:
int fab(int n)
{ if (n<3)
{return 1;}
else
{int first = 1,second = 1,temp = 0;
for (int i =0;i<n-2;i++)
{temp = first + second;
first = second;
second = temp;}
return temp;
}
}
例 1 :一個飼養場引進一隻剛出生的新品種兔子,這種兔子從出生的下一個月開始,每月新生一隻兔子,新生的兔子也如此繁殖。如果所有的兔子都不死去,問到第 12 個月時,該飼養場共有兔子多少只?
分析:這是一個典型的遞推問題。我們不妨假設第 1 個月時兔子的只數為 u 1 ,第 2 個月時兔子的只數為 u 2 ,第 3 個月時兔子的只數為 u 3 ,……根據題意,“這種兔子從出生的下一個月開始,每月新生一隻兔子”,則有
以下是引用片段:
u 1 = 1 , u 2 = u 1 + u 1 × 1 = 2 , u 3 = u 2 + u 2 × 1 = 4 ,……
根據這個規律,可以歸納出下面的遞推公式:
以下是引用片段:
u n = (u n - 1) × 2 (n ≥ 2)* ①
對應 u n 和 u n - 1 ,定義兩個疊代變數y 和 x ,可將上面的遞推公式轉換成如下疊代關係:
以下是引用片段:
y=x*2
x=y
讓計算機對這個疊代關係重複執行 11 次,就可以算出第 12 個月時的兔子數。參考程式如下:
以下是引用片段:
cls
x=1
for i=2 to 12
y=x*2
x=y
next i
print y
end
例 2 :阿米巴用簡單分裂的方式繁殖,它每分裂一次要用 3 分鐘。將若干個阿米巴放在一個盛滿營養參液的容器內, 45 分鐘後容器內充滿了阿米巴。已知容器最多可以裝阿米巴 2 20 個。試問,開始的時候往容器內放了多少個阿米巴?請編程式算出。
分析:根據題意,阿米巴每 3 分鐘分裂一次,那么從開始的時候將阿米巴放入容器裡面,到 45 分鐘後充滿容器,需要分裂 45/3=15 次。而“容器最多可以裝阿米巴 2 20 個”,即阿米巴分裂 15 次以後得到的個數是 2 20。題目要求我們計算分裂之前的阿米巴數,不妨使用倒推的方法,從第 15 次分裂之後的 2 20 個,倒推出第 15 次分裂之前(即第 14 次分裂之後)的個數,再進一步倒推出第 13 次分裂之後、第 12 次分裂之後、……第 1 次分裂之前的個數。
設第 1 次分裂之前的個數為 x 0 、第 1 次分裂之後的個數為 x 1 、第 2 次分裂之後的個數為 x 2 、……第 15 次分裂之後的個數為 x 15 ,則有
以下是引用片段:
x 14 =x 15 /2 、 x 13 =x 14 /2 、…… x n-1 =x n /2 (n ≥ 1)
因為第 15 次分裂之後的個數 x 15 是已知的,如果定義疊代變數為 x ,則可以將上面的倒推公式轉換成如下的疊代公式:
x=x/2 (x 的初值為第 15 次分裂之後的個數 2 20)
讓這個疊代公式重複執行 15 次,就可以倒推出第 1 次分裂之前的阿米巴個數。因為所需的疊代次數是個確定的值,我們可以使用一個固定次數的循環來實現對疊代過程的控制。參考程式如下:
以下是引用片段:
cls
x=2^20
for i=1 to 15
x=x/2
next i
print x
end
例 3 :驗證角谷猜想。日本數學家角谷靜夫在研究自然數時發現了一個奇怪現象:對於任意一個自然數 n ,若 n 為偶數,則將其除以 2 ;若 n 為奇數,則將其乘以 3 ,然後再加 1。如此經過有限次運算後,總可以得到自然數1。人們把角谷靜夫的這一發現叫做“角谷猜想”。
要求:編寫一個程式,由鍵盤輸入一個自然數n ,把 n 經過有限次運算後,最終變成自然數 1 的全過程列印出來。
分析:定義疊代變數為 n ,按照角谷猜想的內容,可以得到兩種情況下的疊代關係式:當 n 為偶數時, n=n/2 ;當 n 為奇數時, n=n*3+1。用 QBASIC 語言把它描述出來就是:
以下是引用片段:
if n 為偶數 then
n=n/2
else
n=n*3+1
end if
這就是需要計算機重複執行的疊代過程。這個疊代過程需要重複執行多少次,才能使疊代變數n 最終變成自然數1 ,這是我們無法計算出來的。因此,還需進一步確定用來結束疊代過程的條件。仔細分析題目要求,不難看出,對任意給定的一個自然數n ,只要經過有限次運算後,能夠得到自然數 1 ,就已經完成了驗證工作。因此,用來結束疊代過程的條件可以定義為:n=1。參考程式如下:
以下是引用片段:
cls
input "Please input n=";n
do until n=1
if n mod 2=0 then
rem 如果 n 為偶數,則調用疊代公式 n=n/2
n=n/2
print "—";n;
else
n=n*3+1
print "—";n;
end if
loop
end
套用實例
疊代法是用於求方程或方程組近似根的一種常用的
算法設計方法。設方程為f(x)=0,用某種
數學方法導出等價的形式x=g(x),然後按以下步驟執行:
⑴ 選一個方程的近似根,賦給變數x0;
⑵ 將x0的值保存於變數x1,然後計算g(x1),並將結果存於變數x0;
⑶ 當x0與x1的差的絕對值還大於指定的精度要求時,重複步驟⑵的計算。
若方程有根,並且用上述方法計算出來的近似根序列收斂,則按上述方法求得的x0就認為是方程的根。上述算法用C程式的形式表示為:
【算法】疊代法求方程的根
以下是引用片段:
{ x0=初始近似根;
do {
x1=x0;
x0=g(x1); /*按特定的方程計算新的近似根*/
} while (fabs(x0-x1)>Epsilon);
printf(“方程的近似根是%f\n”,x0);
}
疊代算法也常用於求方程組的根,令
X=(x0,x1,…,xn-1)
設方程組為:
xi=gi(X) (I=0,1,…,n-1)
則求方程組根的疊代算法可描述如下:
【算法】疊代法求方程組的根
以下是引用片段:
{ for (i=0;i
x=初始近似根;
do {
for (i=0;i
y=x;
for (i=0;i
x=gi(X);
for (delta=0.0,i=0;i
if (fabs(y-x)>delta) delta=fabs(y-x);
} while (delta>Epsilon);
for (i=0;i
printf(“變數x[%d]的近似根是 %f”,I,x);
printf(“\n”);
}
具體使用疊代法求根時應注意以下兩種可能發生的情況:
⑴ 如果方程無解,算法求出的近似根序列就不會收斂,疊代過程會變成死循環,因此在使用疊代算法前應先考察方程是否有解,並在程式中對疊代的次數給予限制;
⑵ 方程雖然有解,但疊代公式選擇不當,或疊代的初始近似根選擇不合理,也會導致疊代失敗。
① N 為兔子的個數, M為月份 (N+N*1)^M-1=2N^M-1 (註解)