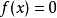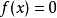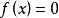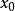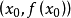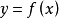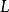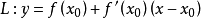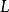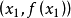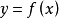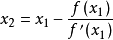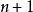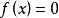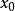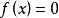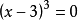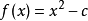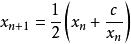基本介紹
- 中文名：牛頓疊代法
- 外文名：Newton's method
- 別稱：牛頓-拉夫遜（拉弗森）方法
- 提出時間：17世紀
產生背景,牛頓疊代公式,其他疊代算法,歐幾里德算法,斐波那契數列,C語言代碼,C++代碼,matlab代碼,定義函式,主程式,Python代碼,Java代碼,JavaScript代碼,Fortran代碼,
產生背景
多數方程不存在求根公式，因此求精確根非常困難，甚至不可能，從而尋找方程的近似根就顯得特別重要。方法使用函式
的泰勒級數的前面幾項來尋找方程
的根。牛頓疊代法是求方程根的重要方法之一，其最大優點是在方程 的單根附近具有平方收斂，而且該法還可以用來求方程的重根、復根，此時線性收斂，但是可通過一些方法變成超線性收斂。另外該方法廣泛用於計算機編程中。
牛頓疊代公式
設
是
的根，選取
作為 的初始近似值，過點
做曲線
的切線
，
，則 與
軸交點的橫坐標
，稱
為 的一次近似值。過點
做曲線 的切線，並求該切線與x軸交點的橫坐標
，稱
為r的二次近似值。重複以上過程，得 的近似值序列，其中，
稱為 的
次近似值，上式稱為牛頓疊代公式。
用牛頓疊代法解非線性方程，是把非線性方程 線性化的一種近似方法。把
在點 的某鄰域內展開成泰勒級數
，取其線性部分（即泰勒展開的前兩項），並令其等於0，即
，以此作為非線性方程 的近似方程，若
，則其解為 ， 這樣，得到牛頓疊代法的一個疊代關係式： 。
已經證明，如果是連續的，並且待求的零點是孤立的，那么在零點周圍存在一個區域，只要初始值位於這個鄰近區域內，那么牛頓法必定收斂。 並且，如果不為0, 那么牛頓法將具有平方收斂的性能. 粗略的說，這意味著每疊代一次，牛頓法結果的有效數字將增加一倍。
疊代法也稱輾轉法，是一種不斷用變數的舊值遞推新值的過程，跟疊代法相對應的是直接法（或者稱為一次解法），即一次性解決問題。疊代算法是用計算機解決問題的一種基本方法。它利用計算機運算速度快、適合做重複性操作的特點，讓計算機對一組指令（或一定步驟）重複執行，在每次執行這組指令（或這些步驟）時，都從變數的原值推出它的一個新值。
利用疊代算法解決問題，需要做好以下三個方面的工作：
一、確定疊代變數
在可以用疊代算法解決的問題中，至少存在一個可直接或間接地不斷由舊值遞推出新值的變數，這個變數就是疊代變數。
二、建立疊代關係式
所謂疊代關係式，指如何從變數的前一個值推出其下一個值的公式（或關係）。疊代關係式的建立是解決疊代問題的關鍵，通常可以使用遞推或倒推的方法來完成。
三、對疊代過程進行控制
在什麼時候結束疊代過程？這是編寫疊代程式必須考慮的問題。不能讓疊代過程無休止地執行下去。疊代過程的控制通常可分為兩種情況：一種是所需的疊代次數是個確定的值，可以計算出來；另一種是所需的疊代次數無法確定。對於前一種情況，可以構建一個固定次數的循環來實現對疊代過程的控制；對於後一種情況，需要進一步分析得出可用來結束疊代過程的條件。
其他疊代算法
歐幾里德算法
最經典的疊代算法是歐幾里德算法，用於計算兩個整數a,b的最大公約數。其計算原理依賴於下面的定理：
定理：gcd(a,b) = gcd(b,a mod b)
證明：a可以表示成a = kb + r，則r = a mod b。假設d是a,b的一個公約數，則有 a%d==0,b%d==0，而r = a - kb，因此r%d==0 ，因此d是(b,a mod b)的公約數
同理，假設d 是(b,a mod b)的公約數，則 b%d==0,r%d==0 ，但是a = kb +r ，因此d也是(a,b)的公約數。
因此(a,b)和(b,a mod b)的公約數是一樣的，其最大公約數也必然相等，得證。
歐幾里德算法就是根據這個原理來做的，歐幾里德算法又叫輾轉相除法，它是一個反覆疊代執行，直到餘數等於0停止的步驟，這實際上是一個循環結構。其算法用C語言描述為：
int Gcd_2(int a,int b)/*歐幾里德算法求a,b的最大公約數*/{if (a<=0 || b<=0)/*預防錯誤*/return 0;int temp;while (b > 0)/*b總是表示較小的那個數，若不是則交換a，b的值*/{temp = a % b;/*疊代關係式*/a = b;b = temp;}return a;}從上面的程式我們可以看到a，b是疊代變數，疊代關係是temp = a % b；根據疊代關係我們可以由舊值推出新值，然後循環執a = b; b = temp；直到疊代過程結束（餘數為0）。在這裡a好比那個膽小鬼，總是從b手中接過位置，而b則是那個努力向前沖的先鋒。
斐波那契數列
還有一個很典型的例子是斐波那契（Fibonacci）數列。斐波那契數列為：0、1、1、2、3、5、8、13、21、…，即 fib⑴=0; fib⑵=1;fib(n)=fib(n-1)+fib(n-2) （當n>2時）。
在n>2時，fib(n)總可以由fib(n-1)和fib(n-2)得到，由舊值遞推出新值，這是一個典型的疊代關係，所以我們可以考慮疊代算法。
int Fib(int n) //斐波那契（Fibonacci）數列{if (n < 1）/*預防錯誤*/return 0;if (n == 1 || n == 2)/*特殊值，無需疊代*/return 1;int f1 = 1,f2 = 1,fn;/*疊代變數*/int i;for(i=3; i<=n; ++i)/*用i的值來限制疊代的次數*/{fn = f1 + f2; /*疊代關係式*/f1 = f2;//f1和f2疊代前進，其中f2在f1的前面f2 = fn;}return fn;}C語言代碼
double func(double x) //函式{ return x*x*x*x-3*x*x*x+1.5*x*x-4.0;}double func1(double x) //導函式{ return 4*x*x*x-9*x*x+3*x;}int Newton(double *x,double precision,int maxcyc) //maxcyc 疊代次數{ double x1,x0; int k; x0=*x; for(k=0;k<maxcyc;k++) { if(func1(x0)==0.0)//若通過初值，函式返回值為0 { printf("疊代過程中導數為0!\n"); return 0; } x1=x0-func(x0)/func1(x0);//進行牛頓疊代計算 if(fabs(x1-x0)<precision || fabs(func(x1))<precision）//達到結束條件 { *x=x1; //返回結果 return 1; } else //未達到結束條件 { x0=x1; //準備下一次疊代 } } printf("疊代次數超過預期！\n"); //疊代次數達到，仍沒有達到精度 return 0;}int main(){ double x,precision; int maxcyc; printf("輸入初始疊代值x0:"); scanf("%lf",&x); printf("輸入最大疊代次數："); scanf("%d",&maxcyc); printf("疊代要求的精度："); scanf("%lf",&precision); if(Newton(&x,precision,maxcyc)==1） //若函式返回值為1 { printf("該值附近的根為：%lf\n",x); } else //若函式返回值為0 { printf("疊代失敗！\n"); } return 0;}C++代碼
//此函式是用來求一元3次方程ax^3+bx^2+cx+d=0的解//比如 x^3-27=0，我們就可以輸入1 0 0 -27，這樣我們就可以得到一個解#include<iostream>#include<cmath>using namespace std;int main(){double diedai(double a,double b,double c,double d,double x);double a,b,c,d;double x=10000.0;cout<<"請依次輸入方程四個係數：";cin>>a>>b>>c>>d;x=diedai(a,b,c,d,x);cout<<x<<endl;return 0;}double diedai(double a,double b,double c,double d,double x){while(abs(a*x*x*x+b*x*x+c*x+d)>0.000001){x=x-(a*x*x*x+b*x*x+c*x+d)/(3*a*x*x+2*b*x+c);}return x;}可以得到一元3次方程3個解的程式(原創，超最佳化)：
#include<iostream>#include<vector>using namespace std;vector<double >v;//stl vector鏈型數組vector<double >::iterator it;//vector疊代器int x0=5;double a,b,c,d;double abs(double y){ while(y<0) y=-y; return y;}double f(double x){ return a*x*x*x+b*x*x+c*x+d;}double fd(double x){ return 3*a*x*x+2*b*x+c;}bool u;//用來判斷是否重複void newton(int a1,int b1,int c1,int d1){ for(x0=-5000;x0<=5000;x0++)//在一個大區域中逐個點用牛頓法，可找出大多數3次方程所有根 { double x1=x0; while(abs(f(x1))>0.001) { double x=x1; x1=x-f(x)/fd(x); } for( it=v.begin();it!=v.end();it++) { if(abs((*it-x1))<0.01) {u=1; break;} } if(u!=1&&x1<1000000000) { cout<<x1<<" "; v.push_back(x1);//把已得到的解添加到vector，用於防止重複 } u=0; } }int main(){ cin>>a>>b>>c>>d; newton(a,b,c,d);}matlab代碼
定義函式
function y=f(x)
y=f(x）；%函式f(x）的表達式
end
function z=h(x)
z=h(x）；%函式h(x）的表達式
end
主程式
x=X;%疊代初值
i=0;%疊代次數計算
while i<= 100%疊代次數
x0=X-f(X)/h(X);%牛頓疊代格式
if abs(x0-X)>0.01；%收斂判斷
X=x0;
else break
end
i=i+1;
end
fprintf('\n%s%.4f\t%s%d'，'X='，X，'i='，i) %輸出結果
Python代碼
Python代碼以實例展示求解方程
的根。
def f(x): return (x-3)**3 '''定義 f(x) = (x-3)^3'''def fd(x): return 3*((x-3)**2) '''定義 f'(x) = 3*((x-3)^2）'''def newtonMethod(n,assum): time = n x = assum Next = 0 A = f(x) B = fd(x) print('A = ' + str(A) + ',B = ' + str(B) + ',time = ' + str(time)) if f(x) == 0.0: return time,x else: Next = x - A/B print('Next x = '+ str(Next)) if A - f(Next) < 1e-6: print('Meet f(x) = 0,x = ' + str(Next)) '''設定疊代跳出條件，同時輸出滿足f(x) = 0的x值''' else: return newtonMethod(n+1,Next)newtonMethod(0,4.0) '''設定從0開始計數，x0 = 4.0'''Java代碼
Java實現開平方的牛頓疊代法. 求
的算術平方根就是求
的正根, 得疊代公式:
. 代碼中取初始值
, 誤差控制在
.
public static double sqrt(double c) { if (c < 0) {return Double.NaN; } double e = 1e-15; double x = c; double y = (x + c / x) / 2; while (Math.abs(x - y) > e) { x = y; y = (x + c / x) / 2; } return x;}JavaScript代碼
/*** @function newtonMethod 該函式是牛頓疊代法的js實現他可以用於求任意一元高次方程的解。（簡單版）* @param fn 要求根的函式* @param dfn 要求根的函式的導函式* @param x0 在函式x定義域上任意取的一個x值x0* @param n 期望疊代的次數* @return 該方程的近似解* */function newtonMethod(fn, dfn, x0, n){ const y = fn(x0) // 在函式有效區間內選取任意 x0 求出點 (x0,y) 其中 y= fn(x0) const k = dfn(x0) // 使用導函式求出過 點(x0,y) 的切線斜率 k const b = y - k * x0 // 將點(x0,y) 代入直線方程 y=kx+b 求出常數 b 。 const x = (0 - b) / k // 將 y=0代入直線方程 y=kx+b 求出該方程的一次近似解 x if(--n > 0){ return newtonMethod(fn, dfn, x, n) // 當n趨於無窮大時得到該方程的精確解 } return x}// 化簡函式 (simplify)function NTMethod(fn = _=>_, dfn = _=>1, x0 = 0, n = 1){ const x = x0 - fn(x0) / dfn(x0) if(n === 1){ return x // 返回一個關於函式 fn(x) 的近似解 } return NTMethod(fn, dfn, x, --n)}Fortran代碼
program newton
implicit none
real::a
real::b
real::fb
real::counter
integer::n
!real,parameter::zero=0.00001
real::fx,fx1
real::df
write(*,*)"enter a number:"
read(*,*)a
do counter=1,a-1
fx=sin(counter)
fx1=sin(counter+1)
if (fx*fx1<0) then
df=cos(counter)
fx=sin(counter)
write(*,*)"初始值取："
write(*,*)counter
do n=1,25,1
b=counter-fx/df
fb=sin(b)
end do
write(*,*)"數值解："
write(*,*)b
end if
end do
stop
end program
