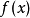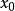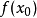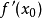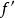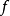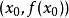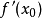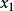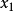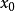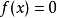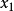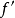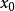牛頓逼近法-牛頓逼近法是牛頓在17世紀提出的一種在實數域和複數域上近似求解方程的方法。多數方程不存在求根公式,因此求精確根非常困難,甚至不可能,從而尋找方程的近似根就顯得特別重要。方法使用函式f(x)的泰勒級數的前面幾項來尋找方程f(x) = 0的根。牛頓疊代法是求方程根的重要方法之一,其最大優點是在方程f(x) = 0的單根附近具有平方收斂,而且該法還可以用來求方程的重根、復根,此時線性收斂,但是可通過一些方法變成超線性收斂。
基本介紹
- 中文名:牛頓逼近法
- 外文名:Newton's method\Newton-Raphson method
- 屬性:牛頓
- 性質:逼近法
- 牛頓法的本質:仍然是“以直代曲”
- 別名:牛頓法、牛頓-拉弗森方法
簡介,起源,方法說明,具體介紹,
簡介
牛頓逼近法,又稱牛頓法(英語:Newton's method)又稱為牛頓-拉弗森方法(英語:Newton-Raphson method),它是一種在實數域和複數域上近似求解方程的方法。方法使用函式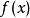 的泰勒級數的前面幾項來尋找方程
的泰勒級數的前面幾項來尋找方程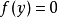 的根。
的根。
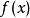
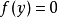
起源
牛頓法最初由艾薩克·牛頓在《流數法》(Method of Fluxions,1671年完成,在牛頓去世後的1736年公開發表)中提出。約瑟夫·鮑易也曾於1690年在Analysis Aequationum中提出此方法。
方法說明
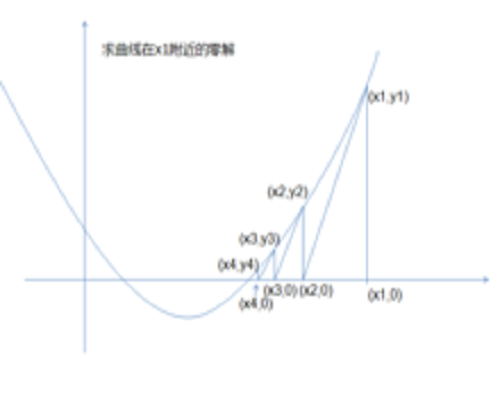
藍線表示方程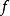 而紅線表示切線。可以看出
而紅線表示切線。可以看出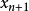 比
比 更靠近
更靠近 所要求的根
所要求的根 。
。
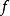
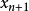



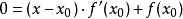
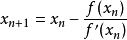
並且,如果 ,那么牛頓法將具有平方收斂的性能。粗略的說,這意味著每疊代一次,牛頓法結果的有效數字將增加一倍。
,那么牛頓法將具有平方收斂的性能。粗略的說,這意味著每疊代一次,牛頓法結果的有效數字將增加一倍。

具體介紹
求代數方程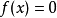 的精確解是很難的事情,特別地當
的精確解是很難的事情,特別地當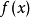 是 高於5次的多項式時,不能通過多項式係數的有限次運算得到根的表達式。在這種情況下求 方程的近似解卻是可以的,牛頓法就是一種比較好的逐次逼近法。牛頓法在求根過程中逼近很快,用計算機計算是十分方便的。
是 高於5次的多項式時,不能通過多項式係數的有限次運算得到根的表達式。在這種情況下求 方程的近似解卻是可以的,牛頓法就是一種比較好的逐次逼近法。牛頓法在求根過程中逼近很快,用計算機計算是十分方便的。
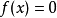
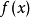
牛頓法的本質仍然是“以直代曲”,首先猜測一個值x1,用它近似方程的根 c,用過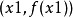 點的切線
點的切線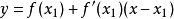 近似代替曲線
近似代替曲線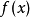 ,然後用切線方程
,然後用切線方程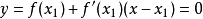 的根
的根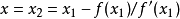 近似代替曲線方程的根c,這樣就得到c的第二個近似值。依此類推可得到疊代公式
近似代替曲線方程的根c,這樣就得到c的第二個近似值。依此類推可得到疊代公式
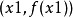
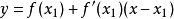
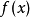
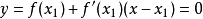
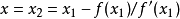
在複平面上選定一個區域,對於任意初始點(除去(0,0)點),討論它在牛頓法疊代過程中的行為。一般選 ,其中p是大於2的正整數。這樣,疊代公式還可以 改寫為
,其中p是大於2的正整數。這樣,疊代公式還可以 改寫為

對於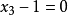 ,有三個根:
,有三個根: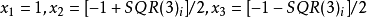 ,三個根均勻地分布在單位圓上。
,三個根均勻地分布在單位圓上。
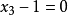
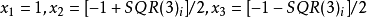
疊代過程照例要先將複數分解為實部和虛部:
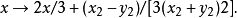
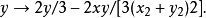
以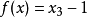 為例,用牛頓法生成分形圖形的一個簡單的matlab源程式如下:
為例,用牛頓法生成分形圖形的一個簡單的matlab源程式如下:
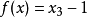
% 牛頓求根法
N=160;
warning off
[X,Y]=meshgrid((-N:N)/N*2);
[m,n]=find(X==0&Y==0);
X(m,n)=1;
Y(m,n)=1;
R=zeros(321);
G=R;
B=R;
for k=1:30;
Xn=2*X/3+(X.^2-Y.^2)./(3*(X.^2+Y.^2));
Yn=2*Y/3-2*X.*Y./(3*(X.^2+Y.^2));
X=Xn;
Y=Yn;
end
R(X>0.8)=1;
G(Y<-0.5)=1;
B(Y>0.5)=1;
imshow(cat(3,R,G,B))