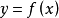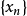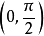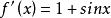切線法是通過曲線上的一些特徵點的切線的交點坐標關係來計算磁性體的產狀。
基本介紹
方程求根方法





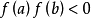

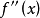



收斂性的證明







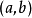
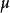
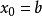



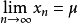

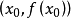








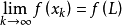







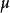
計算實例
求方程實根
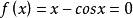
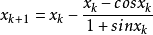
x0 | 1 |
x1 | 0.75036386784024 |
x2 | 0.73911289091136 |
x3 | 0.73908513338528 |
x4 | 0.73908513321516 |
x5 | 0.73908513321516 |
#include "math.h"#include "stdio.h"#define ABS(a) ((a)<0?-(a):(a))static double f(double x){ return x-cos(x);}static double df(double x){ return 1+sin(x);}void main(){ int i; double x0=1, x1, err=1e-14; for(i=1; i<50; i++) { x1=x0-f(x0)/df(x0); printf("x[%d]=%.14f\n", i, x1); if(ABS(x1-x0)<err) break; x0=x1; }}任意數開n次方

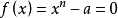

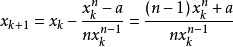

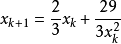
x0 | 2 |
x1 | 3.75000000000000 |
x2 | 3.18740740740741 |
x3 | 3.07642248706644 |
x4 | 3.07232230248782 |
x5 | 3.07231682569561 |
x6 | 3.07231682568585 |
x7 | 3.07231682568585 |
// 2015-12-24// By: ChenYu#include "math.h"#include "stdio.h"#define ABS(a) ((a)<0?-(a):(a))#ifdef _WIN32 typedef unsigned __int64 uint64;#else typedef unsigned long long uint64;#endif// calculate a approximate valuestatic double calcInitRoot(double x, int n){ const uint64 exptMask=((uint64)1<<11)-1; const uint64 fracMask=((uint64)1<<52)-1; uint64 xInt=*(uint64*)&x; int xExpt=(int)((xInt>>52)&exptMask)-1023; xInt=((uint64)((xExpt+1024*n-1)/n)<<52)+(xInt&fracMask)/n; return *(double*)&xInt;}double calcRoot(double x, int n){ int i, j, s=1-((x<0)<<(n&1)); double a=ABS(x); double x1, x0=calcInitRoot(a, n); double err=x0*1e-14; if(x==0) return 0; for(i=1; i<50; i++) { double xn=1; for(j=0; j<n-1; j++) xn*=x0; x1=((n-1)*x0*xn+a)/(xn*n);// printf("x%d=%.14f\n", i, x1); if(ABS(x1-x0)<=err) break; x0=x1; } return s*x1;}void main(){ double x=-31141.592653589793; int n=11; double y=calcRoot(x, n); printf("root(%g,%d)=%+.14f\n", x, n, y); printf("root(%g,%d)=%+.14f\n", x, n, pow(ABS(x), 1.0/n));}