基本介紹
- 中文名:切線方程
- 外文名:tangent line equation
- 證明方法:向量法
- 類別:數學領域
定義
方程的證明
向量法





分析-解析法
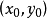
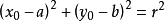
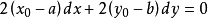




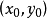




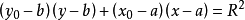
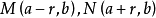

常見切線方程的證明
圓
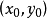

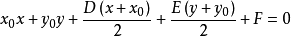
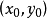


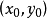


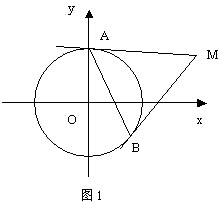 過圓外一點的2條切線
過圓外一點的2條切線橢圓

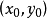



雙曲線
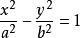
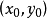
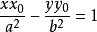
拋物線

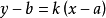
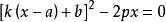
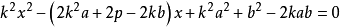


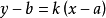


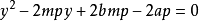



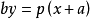


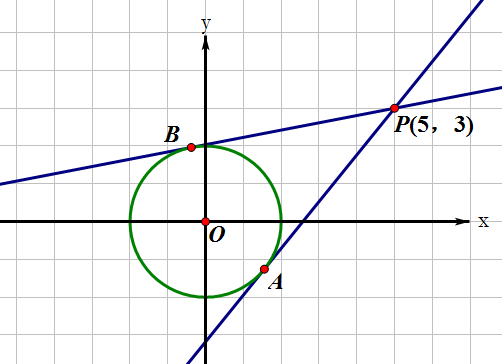





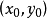
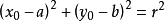
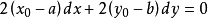




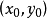




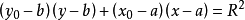
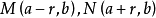

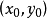

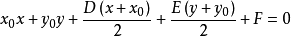
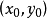


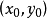


 過圓外一點的2條切線
過圓外一點的2條切線
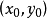



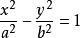
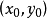
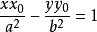

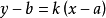
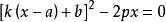
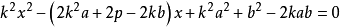


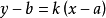


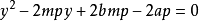



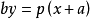


切線方程是研究切線以及切線的斜率方程,涉及幾何、代數、物理向量、量子力學等內容。是關於幾何圖形的切線坐標向量關係的研究。分析方法有向量法和解析法。...
對於直線,法線是它的垂線;對於一般的平面曲線,法線就是切線的垂線;對於空間圖形,是垂直平面。...
切線法是通過曲線上的一些特徵點的切線的交點坐標關係來計算磁性體的產狀。...... 切線法是通過曲線上的一些特徵點的切線...的切線,則切線方程為:上述切線與 軸的...
圓的標準方程(x-a)²+(y-b)²=r²中,有三個參數a、b、r,即圓心坐標為(a,b),只要求出a、b、r,這時圓的方程就被確定,因此確定圓方程,須三個...
拋物線y1=2px上一點(x0,y0)處的切線方程為: 。拋物線y1=2px上過焦點斜率為k的方程為:y=k(x-p/2)。拋物線相關參數 編輯 ...
法平面是數學術語,是指過空間曲線的切點,且與切線垂直的平面,稱為法平面。即垂直於虛擬法線的平面。例如,球體的中心為端點的射線,與球面所在的每一切點所在的切面...
H = 0的情況可以作為退化消除,因此C的切線方程可以寫為P + fQ = 0,其中f是任意多項式m-2例如,令P1 =(1,0),P2 =( - 1,0)。切線方程為X + 1 = ...
垂足曲線(pedal curve)是一種平面曲線,即由一已知曲線所產生的另一曲線。給定一條曲線C和一個定點O,從點O向曲線C的任一條切線作垂線,垂足M的軌跡S稱為曲線C...
過圓錐曲線上一點 (x0,y0)的切線方程 x0·x/a²+y0·y/b²=1 x0x/a²-y0·y/b²=1 y0·y=p(x+x0) 斜率為k的切線方程 y=kx±√...
點斜式是指一種算式,已知直線上一點(a,b)並且存在直線的斜率k,則直線可表示y-b=k(x-a)。點斜式方程是通過直線過的一個點和其斜率求該直線平面方程的一...
過圓錐曲線上一點 (x0,y0)的切線方程 x0·x/a²+y0·y/b²=1 x0x/a²-y0·y/b²=1 y0·y=p(x+x0) 斜率為k的切線方程 y=kx±√...
在幾何學中,在給定點處的平面曲線的切線是在該點處“剛好接觸”曲線的直線。萊布尼茲將其定義為通過曲線上一對無限封閉的點的線。更準確地說,如果直線通過曲線上...
表示一條直線(或曲線的切線)關於(橫)坐標軸傾斜程度的量。它通常用直線(或曲線的切線)與(橫)坐標軸夾角的正切,或兩點的縱坐標之差與橫坐標之差的比來表示。...
