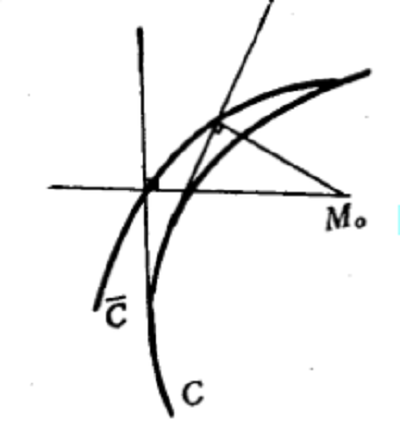
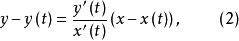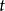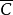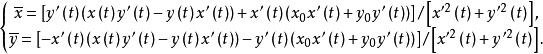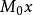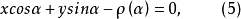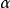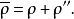垂足曲線(pedal curve)是一種平面曲線,即由一已知曲線所產生的另一曲線。給定一條曲線C和一個定點O,從點O向曲線C的任一條切線作垂線,垂足M的軌跡S稱為曲線C關於O點的垂足曲線。反過來,C稱為曲線S關於O點的反垂足曲線。例如,拋物線關於焦點的垂足曲線是直線,橢圓和雙曲線關於焦點的垂足曲線都是圓,等邊雙曲線關於中心的垂足曲線是雙紐線。
基本介紹
- 中文名:垂足曲線
- 外文名:pedal curve
- 所屬學科:數學
- 所屬問題:平面解析幾何(平面曲線)
- 相關概念:切線、垂線等
定義
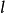



垂足曲線的方程


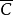



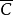
 圖1
圖1