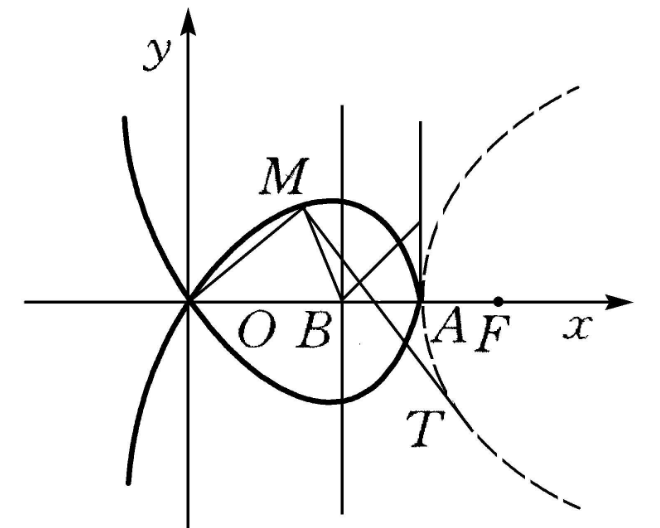
麥克勞林三等分角線

麥克勞林三等分角線(Maclaurin trisectrix)又名馬克勞林三等分角線，是在笛卡爾直角坐標中方程式x³+xy²+ay²-3ax²=0的平面曲線(拋物線的垂足曲線)，是史路士蚌線的特殊情況(若那裡k²=4a²)。

基本介紹

• 中文名：麥克勞林三等分角線
• 外文名：Maclaurin trisectrix
• 別名：馬克勞林三等分角線
• 所屬學科：數學（平面幾何）
• 相關概念：三等分角問題，幾何三大難題

基本介紹

麥克勞林三等分角線是可用於將一角三等分的平面曲線，從拋物線的焦點F關於準線的對稱點O，引此拋物線的切線的垂線，垂足的軌跡叫做麥克勞林三等分角線。設OF=4a，拋物線的方程為y=4a(x-3a)，則麥克勞林三等分角線的方程為x(x²+y²)+a(y²-3x²)=0。

若取點B(2a，0)為極點，BF為極軸，則方程可化為ρ cos(θ/3)=a，在麥克勞林三等分角線上任取點M(ρ，θ)作以極半徑ρ為斜邊，定長a為直角邊的直角三角形ABC，則∠ABC=θ/3，因而可用於將角θ三等分。

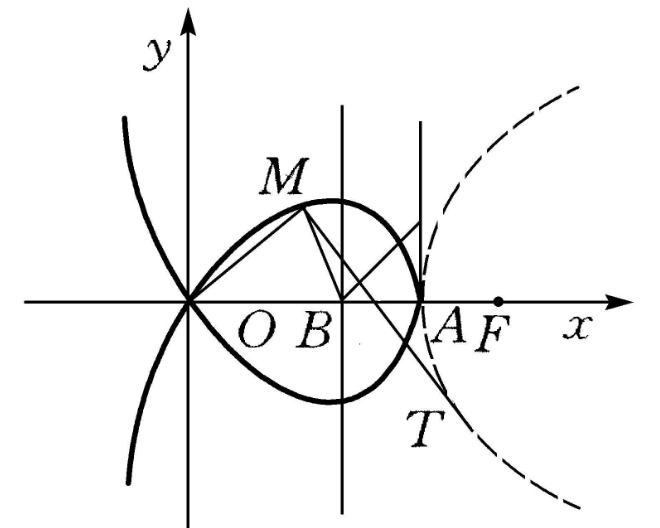圖1 麥克勞林三等分角線

三等分角線

解釋：（1）三等分角線是由x³+xy²+ay²-3ax²=0確定的平面曲線，可用來解決三等分角問題。它是由馬克勞林(C.Maclaurin，蘇格蘭，1698—1746)提出的。、

（2）三等分角線是一種特殊曲線，指可用於將角三等分的曲線。例如，蚌線、阿基米德螺線等都是三等分角線。

三等分角問題

三等分角問題是希臘三大幾何作圖問題之一，即僅用直尺與圓規是否可以三等分任意角。限定直尺只能過一點或兩點畫直線，圓規只能在已知圓心、半徑時畫圓。

1837年，法國數學家旺策爾(P.-L.Wantzel)證明了可尺規作圖的量必須滿足一個2次的方程，進而推出：在一般情況下，尺規三等分任一角是不可能的.這裡的結論是有一定限制的，限定“一般情況下”，因為存在無窮多個角是可以尺規三等分的.例如，可以證明：當m，n是互素的正整數，且n不能被3整除時，角

或

是可以尺規三等分的.顯然，這樣的α有無窮多。

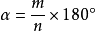
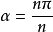
尺規作圖三等分任一角，只能得到近似值.近似三等分任意角的尺規作圖中，精度較高且作圖簡單的當屬拉姆(J.F.Lamb)在1988年給出的作圖(見圖1).設∠AOB為已知角，以O為圓心畫圓弧交兩邊於A，B，BO的延長線交圓於D.作∠AOB的平分線OC，取OD的中點E，連結EC，則

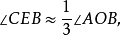
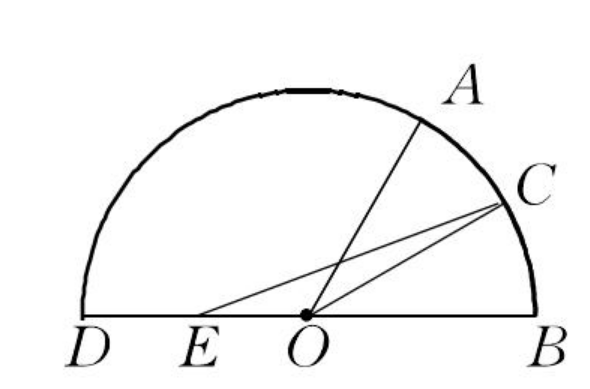圖1

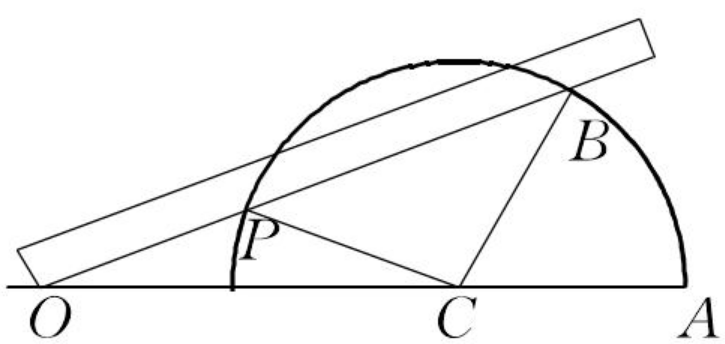圖2

經計算，當∠AOB≤90°時，

如果不限定尺規作圖，則最簡單的三等分角的方法是古希臘數學家阿基米德(Archimedes)給出的，如圖2所示.在直尺邊緣上添加一點P，命尺端為O.設所要三等分的角是∠ACB，以C為圓心，OP為半徑作半圓交角邊於A，B.使點O在AC延長線上移動，使點P落在圓周上且使尺通過點B，連結OB.由於OP=PC=CB，則

德國數學家比伯巴赫(L.Bieberbach)證明了：如果使用直角尺和圓規，則可以三等分任一角.1982年，鄧肯(E.B.Dynkin)和巴尼厄(W.Barnier)證明了：在一般情況下，尺規作圖p等分任意角是不可能的，其中p為奇素數.

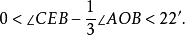
幾何三大“難題”

幾何三大“難題”是古希臘人提出的三個(初等)幾何學的著名“難題”：三等分角問題、倍立方問題及化圓為方問題。即要求用圓規與直尺分別實現：

(1)三等分一個任意角;

(2)作一個立方體，使它的體積等於已知立方體的兩倍;

(3)作一正方形，使它的面積等於已知圓的面積。

1837年萬策爾給出了前兩個問題不可能性的證明;

1882年，林德曼證明了π為超越數，由此得出化圓為方問題的不可能性。因此，這三個問題是不可能問題，而不是難題。數學愛好者不要為此耗費精力。

如果取消只用尺規作圖的限制，例如利用刻度尺、量角器或某些曲線(如三等分角線、割圓曲線等)，就可以解決這些問題。