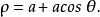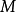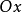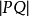蚌線是一種特殊曲線。沿給定平面曲線C:ρ=f(θ)的極徑方向增加或減少一個定長線段b,這樣得到的曲線ρ=f(θ)±b稱為曲線C的蚌線,或稱為一般蚌線,圓的蚌線就是帕斯卡蝸線。
直線l的蚌線稱為尼科米迪斯蚌線,通常的蚌線就是指尼科米迪斯蚌線,它的極坐標方程是ρ=a sec θ±b,蚌線有兩支,都以定直線l為漸近線,一支與定點O位於定直線的同側,稱為蚌線的內支,另一支與定點O位於定直線的異側,稱為蚌線的外支。它們都關於極軸對稱,在廣義極坐標系下,方程ρ=a sec θ+b與ρ=a sec θ-b表示相同的曲線,化為直角坐標方程就是(x2+y2)(x-a)2=b2x2,這方程表示的曲線,當a>b時含有一個孤立點O,當a=b或a<b時,原點O是尖點或結點,尼科米迪斯(Nicomedes)在研究任意角三等分時發現了蚌線。
基本介紹
- 中文名:蚌線
- 外文名:Conchoid
- 發現人:尼科米迪斯
- 舉例:尼科米茲蚌線、蝸牛線等
基本概念
尼科米茲蚌線
 圖1直線的蚌線
圖1直線的蚌線定義



 圖2
圖2尼科米茲蚌線的極坐標方程


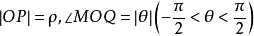

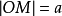
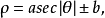




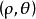

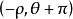

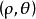
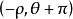


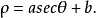
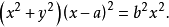
 圖3
圖3
 圖4(a)
圖4(a) 圖4(b)
圖4(b) 圖4(c)
圖4(c)蝸牛線
定義
 圖5
圖5蝸牛線的極坐標方程
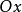
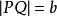
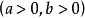

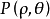
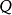
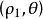
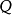
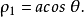
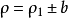

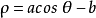
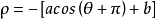

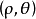
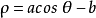

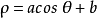

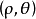
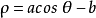
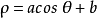

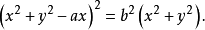
蝸牛線的分類

 圖6 長心臟線 a>b
圖6 長心臟線 a>b 圖7 心臟線 a=b
圖7 心臟線 a=b
 圖 8 短心臟線 a<b
圖 8 短心臟線 a<b心臟線的極坐標方程