現有平面上的一條直線L和直線外的一點P,過點P畫與直線L相交的射線,在每條射線上,以直線L為界截取長度為a(a是一正有理數)的一段,這些線段的端點所形成的曲線稱為尼科梅德斯蚌線或蚌線。如圖:

尼科梅德斯蚌線的
極坐標方程為r=a+b·secθ。
尼科梅德斯蚌線是尼科梅德斯在努力解決
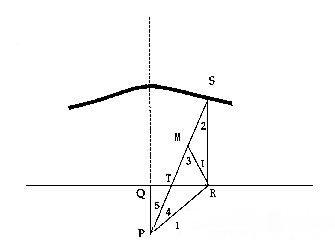
三等分角這一古希臘幾何作圖題時發現的。所以三等分一個角可以用蚌線解決:取∠P為直角三角形△QPR的一個銳角。以P為極點,QR為固定線L畫一條蚌線,使得它由L向外截出的固定長度等於斜邊長|PR|的兩倍。在R點作RS⊥QR並交蚌線於S點。現∠QPT即為∠QPR的三分之一(T為PS與QR的交點)。如圖: