點斜式是指一種算式,已知直線上一點(a,b)並且存在直線的斜率k,則直線可表示y-b=k(x-a)。
點斜式方程是通過直線過的一個點和其斜率求該直線平面方程的一種方法。在平時做解析幾何的題目時,會更多地運用點斜式方程來解題,直接的體現直線的性質。
基本介紹
- 中文名:點斜式
- 外文名:Point oblique type
- 適用範圍:數理科學
- 點斜式::y-y1=k(x-x1)
- 套用鄰域:解析幾何
定義,套用,推導,方程用途,
定義



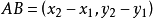

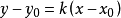
套用
y2-y1=k(x2-x1)
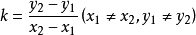
當直線與x軸垂直時,k不存在時,直線可表示為

當直線與y軸垂直時,k=0時,直線可表示為

局限性:當α為π/2即直線與X軸垂直時,tanα無意義,不存在點斜式方程。
推導
若直線 經過點
經過點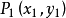 ,且斜率為k,求L1方程。
,且斜率為k,求L1方程。

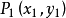
設點P(x,y)是直線上不同於點P1的任意一點,直線 的斜率應等與直線
的斜率應等與直線 的斜率,根據經過兩點的直線的斜率公式得
的斜率,根據經過兩點的直線的斜率公式得



所以,直線 :
:


說明:
(1)這個方程是由直線上一點和斜率確定的,這一點必須在直線上,否則點斜式方程不成立;
(3)當直線傾斜角為90°時,直線沒有斜率,它的方程不能用點斜式表示,這時直線方程為 。
。

方程用途
開始學習時通常是求兩條斜率不相等(非平行)的直線的交點,接著是與拋物線的交點,通過點斜式方程代入拋物線方程,求出交點的個數和坐標。還有平面解析幾何,比如橢圓、圓、雙曲線、拋物線等圓錐曲線問題解決的固定套路,方程聯立的時候就習慣用點斜式。
另外,有時題目會告訴曲線外一點(a,b)和曲線方程,這時只需設切點坐標A(x,y),利用導數公式求出導數的表達式M,再使 即可求出切點A的坐標。利用點斜式可將方程表示出來。
即可求出切點A的坐標。利用點斜式可將方程表示出來。


