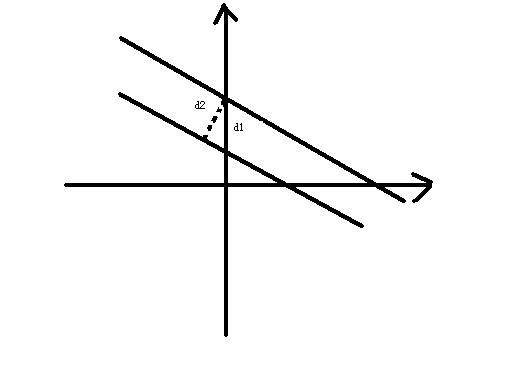
基本介紹
- 中文名:斜截式
- 外文名:slope intercept form
- 形式:y=kx+b
- 幾何意義:k為斜率,b為y軸截距
- 領域:解析幾何
- 適用條件:直線不與y軸平行
直線的表達形式,斜截式,
直線的表達形式
直線方程常用的表達形式主要有點斜式、斜截式、兩點式和截距式。

當已知斜率 和y軸截距
和y軸截距 時,常用斜截式:
時,常用斜截式:



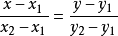

斜截式
已知直線在y軸上的截距為 ,斜率為
,斜率為 ,可以確定該直線的方程。
,可以確定該直線的方程。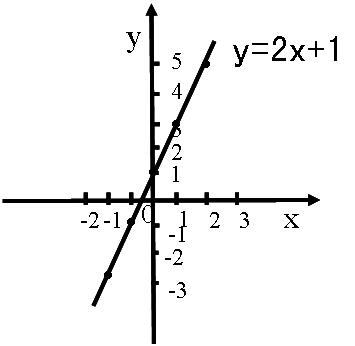



即已知直線的斜率 ,且該直線過點
,且該直線過點 ,利用點斜式方程,將坐標代入得
,利用點斜式方程,將坐標代入得



即




顯然斜截式是點斜式方程的一種特殊情況,也是直線表達式的一種重要形式。
考慮一下兩種特殊情況:
①當直線與 軸平行時,斜率
軸平行時,斜率 ,直線到
,直線到 軸的距離為
軸的距離為 。
。




②當直線與 軸平行時,斜率
軸平行時,斜率 不存在,所以此時直線不能用斜截式表示,但是容易看出,直線與
不存在,所以此時直線不能用斜截式表示,但是容易看出,直線與 軸相交,記交點為
軸相交,記交點為 ,則直線方程為
,則直線方程為 。
。