兩點式

兩點式是直線方程的一種表達形式，是解析幾何直線理論的重要概念。

直線方程的常用表示形式有點斜式、斜截式、兩點式和截距式，當一隻直線上兩點坐標時，常用兩點式來表示直線方程。在二維坐標系中，兩點式的表達公式是(y-y2)/(y1-y2) = (x-x2)/(x1-x2)。

基本介紹

• 中文名：兩點式
• 外文名：Two-point Form
• 定義：用直線上兩點坐標表示的直線方程
• 套用條件：已知直線上兩點坐標
• 表達式：(y-y2)/(y1-y2)=(x-x2)/(x1-x2)
• 套用領域：解析幾何

直線的表達形式

直線方程常用的表達形式主要有點斜式、斜截式、兩點式和截距式。

點斜式（用於已知斜率和一點坐標）

斜截式（用於已知斜率和y軸截距）

兩點式（用於已知兩點坐標）

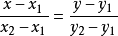
截距式（用於已知所有截距）

兩點式推導

我們知道，通過兩不同點的直線有且只有一條。設兩個不同的點 決定唯一的一條直線 ，此時我們可以取該直線的方向向量

從而直線 的方程可以表示為

此方程稱為直線的兩點式方程。

此式也可用行列式的形式表現為 。

例如，過點 和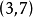 的直線方程可以用兩點式表示為：

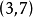
適用範圍

是不是已知任意直線上兩點就能用兩點式寫出直線方程呢？答案是否定的。當或時，直線方程不能用兩點式表示，因為此時兩點式的分母為0，方程無意義。即兩點式方程不能用來表示坐標軸或與坐標軸平行的直線。

套用

利用兩點式方程，很容易得到三個點 在同一條直線上的充分必要條件是