過原點向直線做一條的垂線段,該垂線段所在直線的傾斜角為α,p是該線段的長度。 x·cos α+ysin α-p=0。 規定:與X軸平行或重合的直線的傾斜角為0°
基本介紹
- 中文名:法線式
- 外文名:Normal form
- 適用範圍:數理科學
- 套用鄰域:解析幾何
- 方程式:xcosα+ysinα-p=0
定義,推導方法,斜截式推導,兩點式推導,截矩式推導,勾股定理推導,
定義
過原點向直線做一條的垂線段,該垂線段所在直線的傾斜角為α,p是該線段的長度。則該直線方程的法線式為:xcosα+ysinα-p=0。其中p為原點到直線的距離,θ為法線與X軸正方向的夾角。
推導方法
斜截式推導
設坐標平面內的任意一條直線l在y 軸上的截距為b,法線n交直線l於點N,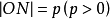 ,x軸的正方向到法線n的正方向的角為θ,則直線l和y軸的交點B的坐標與點N的坐標分別為(0,b)與(psinθ,pcosθ)(圖一)
,x軸的正方向到法線n的正方向的角為θ,則直線l和y軸的交點B的坐標與點N的坐標分別為(0,b)與(psinθ,pcosθ)(圖一) 圖一
圖一
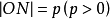
 圖一
圖一由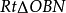 得
得
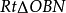
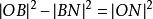
故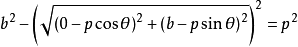
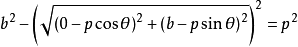
解得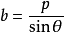
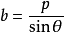
又由法線n的斜率 知
知

直線l的斜率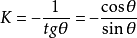
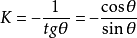
將這裡的K和b的值代入直線方程的斜截式得
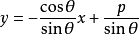
若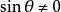 ,方程兩端都乘以
,方程兩端都乘以 後,將各項都移至等號左邊得
後,將各項都移至等號左邊得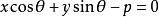
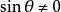

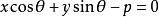
若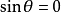 ,仍有
,仍有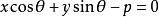
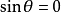
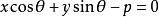
兩點式推導
因直線l經過點N(pcosθ,psinθ)及點B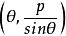 (圖一),故
(圖一),故
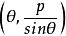
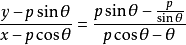
因此
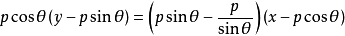

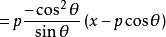
兩邊都乘以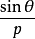 後,展開得
後,展開得
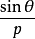
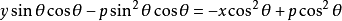
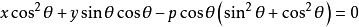
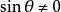
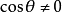
所以

截矩式推導
設直線l在x軸上的截距為a(圖一),用與求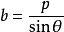 類似的方法可求得
類似的方法可求得
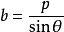
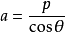
將這裡的a和b的值代入直線方程的截距式得
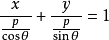
整理得

勾股定理推導
設P(x,y)為直線上的任意一點( 下文中的p皆與此意義同),則圖一中:
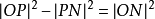
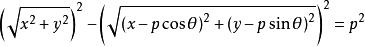
兩邊平方並整理得


