“平面方程”是指空間中所有處於同一平面的點所對應的方程,其一般式形如Ax+By+Cz+D=0。
基本介紹
- 中文名:平面方程
- 外文名:Planar Equation
- 分類:截距式、點法式、一般式、法線式
- 學科領域:數學
- 名詞屬性:數學術語
- 截距式:x/a+y/b+z/c=1
- 點法式:A(x-x0)+B(y-y0)+C(z-z0)=0
- 一般式:Ax+By+Cz+D=0
- 法線式:xcosα+ycosβ+zcosγ=p
定義
類型
一、截距式
二、點法式

“平面方程”是指空間中所有處於同一平面的點所對應的方程,其一般式形如Ax+By+Cz+D=0。

“平面方程”是指空間中所有處於同一平面的點所對應的方程,其一般式形如Ax+By+Cz+D=0。...
法平面是數學術語,是指過空間曲線的切點,且與切線垂直的平面,稱為法平面。即垂直於虛擬法線的平面。例如,球體的中心為端點的射線,與球面所在的每一切點所在的切面...
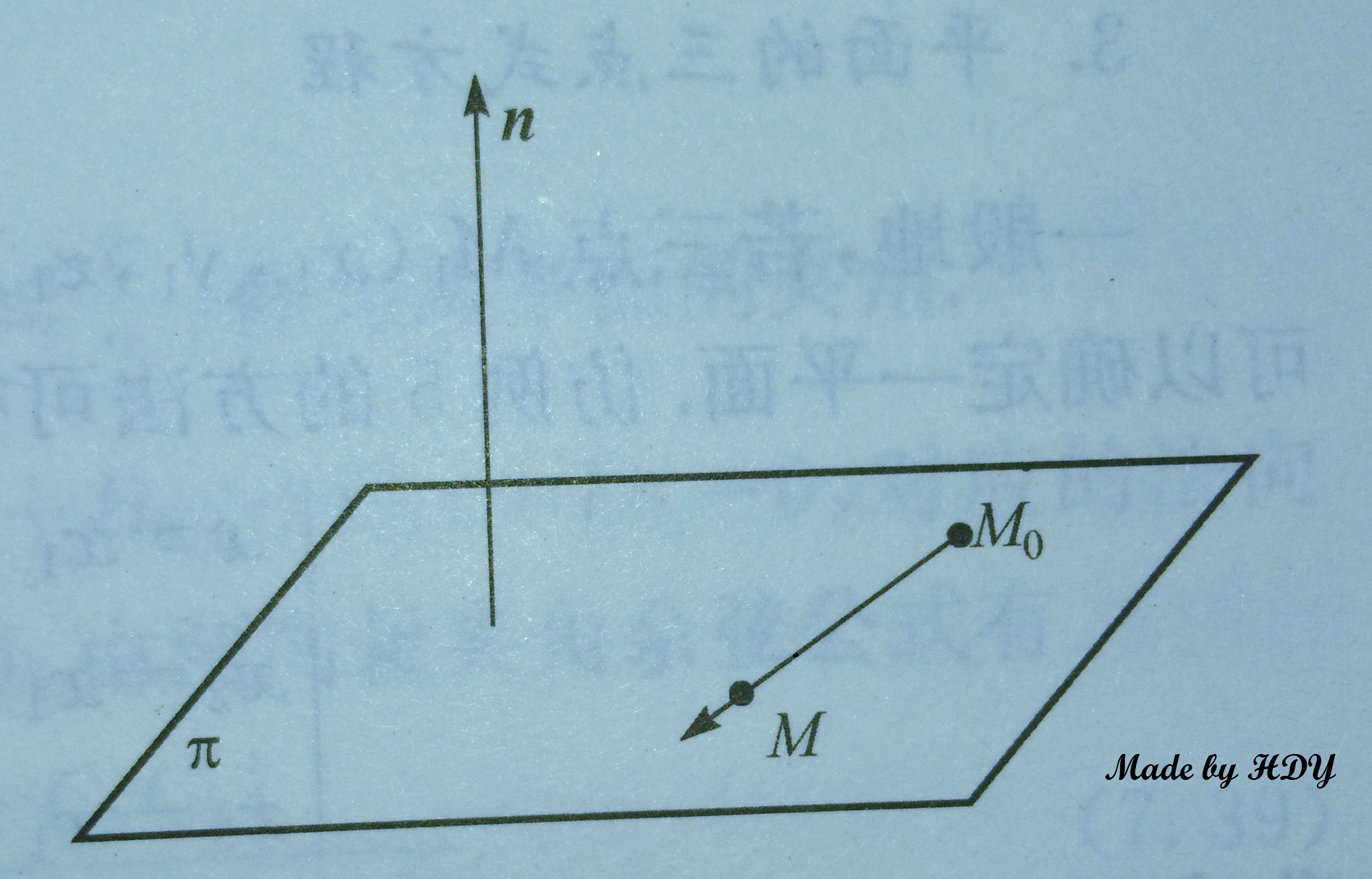
平面的點法式方程(point normal form equatio-n of a plane)是平面方程的一種形式.在空間直角坐標系中,給定一點M(x0,y0,z0)和平面上的一個法向量n=(A,B...
在空間中,到兩點距離相同的點的軌跡。在中,平面公式為A*(x-x0)+B*(y-y0)+C*(z-z0)=0,其定義為與固定點(x0,y0,z0)的連線垂直於固定方向(A,B,C)...
平面方程的三種形式之一,另兩種是平面的一般方程和平面的點法式方程。...... 平面方程的三種形式之一,另兩種是平面的一般方程和平面的點法式方程。中文名 平面截距...
平面π上任意一點的坐標都滿足這個方程。而坐標滿足方程的點都在π上。於是這個方程就是過點且與向量垂直的平面π的方程,稱為平面的點法式方程。...
平面把(bundle of planes)亦稱平面叢,是一種空間圖形,空間一定點的所有平面組成的集合稱為平面把。這個定點稱為平面把的中心,另一種平面把是平行於同一條直線(...
在數學中,平面曲線是可以是歐幾里德平面、仿射平面或投影平面中的曲線。 最常研究的情況是平滑平面曲線(包括分段平滑曲線)和代數平面曲線。...
從平面解析幾何的角度來看,平面上的直線就是由平面直角坐標系中的一個二元一次方程所表示的圖形。求兩條直線的交點,只需把這兩個二元一次方程聯立求解,當這個...
在電化學中,Cottrell方程描述了在受控電位實驗中電流相對於時間的變化...... Cottrell方程描述了平面的電極的情況,但也可以通過使用相應的拉普拉斯運算元和邊界條件結合Fic...
平面劃分空間是幾何學的基本概念,平面將其所在空間分割為兩部分。...... 平面劃分空間(cutting space by plane).在空間仿射坐標系中,一個平面方程為 [1] :...
平面極坐標系坐標系的一種。極坐標系在平面內由極點、極軸和極徑組成的坐標系。在平面上取一定點o,稱為極點,由o出發的一條射線ox,稱為極軸。對於平面上任意一...
主應力空間內通過坐標原點且以σ1=σ2=σ3的等傾線為外法線的平面。該平面的方程為σ1+σ2+σ3=0在π平面上,平均應力σm=0,且三個主應力軸在該平面上...
有向平面(directed plane)是一種規定了方向的平面。給平面的垂線規定一個正向,且平面的所有垂線的正向都指向平面的同側,這種規定了垂線正向的平面稱為有向平面。...
共面,又稱共平面,幾何學術語,是指幾何形狀在三維空間中共占同一平面的關係。...... 在一條直線上的三個點可以確定一個平面,可以通過待定係數法求出一個平面方...
