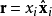方向餘弦

方向餘弦是指在解析幾何里，一個向量的三個方向餘弦分別是這向量與三個坐標軸之間的角度的餘弦。兩個向量之間的方向餘弦指的是這兩個向量之間的角度的餘弦。

“方向餘弦矩陣”是由兩組不同的標準正交基的基底向量之間的方向餘弦所形成的矩陣。方向餘弦矩陣可以用來表達一組標準正交基與另一組標準正交基之間的關係，也可以用來表達一個向量對於另一組標準正交基的方向餘弦。

基本介紹

• 中文名：方向餘弦
• 外文名：direction cosine
• 領域：解析幾何
• 對象：有向線段或相應的有向線段
• 套用學科：數學
• 相關術語：餘弦

空間解釋

設有空間兩點，若以P₁為始點，另一點P₂為終點的線段稱為有向線段。通過原點作一與其平行且同向的有向線段，將與Ox,Oy,Oz三個坐標軸正向夾角分別記作α,β,γ。這三個角α,β,γ稱為有向線段的方向角，其中0≤α≤π,0≤β≤π,0≤γ≤π。若有向線段的方向確定了，則其方向角也是唯一確定的。

方向角的餘弦稱為有向線段或相應的有向線段的方向餘弦。

解析幾何

在解析幾何里，一個向量的三個方向餘弦分別是這向量與三個坐標軸之間的角度的餘弦。

假設 是三維空間裡的向量：

；

其中， 是一組標準正交基的單位基底向量， 分別為 對於x-軸、y-軸、z-軸的分量。

那么， 對於x-軸、y-軸、z-軸的方向餘弦 分別為

其中， 分別為 對於x-軸、y-軸、z-軸的角度。

注意到以下恆等式：

加以推廣，兩個向量之間的方向餘弦指的是這兩個向量之間的角度的餘弦。“方向餘弦矩陣”是由兩組不同的標準正交基的基底向量之間的方向餘弦所形成的矩陣。方向餘弦矩陣可以用來表達一組標準正交基與另一組標準正交基之間的關係，也可以用來表達一個向量對於另一組標準正交基的方向餘弦。

剛體取向

通常，整個剛體的空間位形可以簡易地以以下參數設定：

1. 剛體的“位置”：挑選剛體內部一點G來代表整個剛體，通常會設定物體的質心或形心為這一點。從空間參考系S觀測，點G的位置就是整個剛體在空間的位置。表示位置可以套用向量的概念。向量的起點為參考系S的原點，終點為點G。設定剛體的位置需要三個坐標，例如，採用直角坐標系，這三個坐標為x-坐標、y-坐標、z-坐標。這用掉了三個自由度。
2. 剛體的取向：描述剛體取向的方法有好幾種，包括方向餘弦、歐拉角、四元數等等。這些方法設定一個附體參考系B的取向（相對於空間參考系S）。附體參考系是固定於剛體的參考系。相對於剛體，附體參考系的取向固定不變。由於剛體可能會呈加速度運動，所以附體參考系可能不是慣性參考系。空間參考系是某設定慣性參考系，例如，在觀測飛機的飛行運動時，附著于飛機場控制塔的參考系可以設定為空間參考系，而附著于飛機的參考系則可設定為附體參考系。剛體的取向需要用到另外三個自由度。

方向餘弦方法可以用來設定附體參考系B的取向，即剛體的取向。假設沿著參考系S的坐標軸的三個單位向量分別為 ，沿著參考系B的坐標軸的三個單位向量分別為。定義與之間的方向餘弦為

；

其中，是 與之間的夾角。

與之間的關係分別為

、

、

。

兩個參考系的坐標軸所形成的矩陣稱為“方向餘弦矩陣” A ：

。

採用愛因斯坦求和約定，由於 ，給定方向餘弦矩陣A ，則可設定附體參考系B的取向，也就是剛體的取向。

反過來，經過一番運算，可以得到 。

給定位置向量

，

則與 的內積為

。

方向餘弦矩陣A可以將從空間參考系S觀測的位置坐標，變換為從附體參考系B觀測的位置坐標，因此又稱為“變換矩陣”。

變換矩陣 A 也可以做反變換如下：

。

變換矩陣 A是一種正交矩陣，滿足“正交條件”

；

其中，是克羅內克函式。

注意到與不同，夾角 是與空間參考系S的坐標軸單位向量 之間的夾角。變換矩陣A通常不是對稱矩陣。

變換矩陣A 可以視為旋轉矩陣。例如，將附體參考系B或剛體旋轉，從 旋轉角弧成為；其中， 。對於這旋轉，旋轉矩陣A為

。

參考軸與 之間的關係為

。

旋轉矩陣A也可以視為將點P的位置向量 旋轉 角弧成為點P'的位置向量 ：

。