基本介紹
- 中文名:對稱矩陣
- 外文名:Symmetric Matrices
- 定義:元素以主對角線為對稱軸對應相等
- 性質:對稱矩陣的轉置等於其本身
- 形狀:n 階方陣
- 線性運算:滿足
- 套用科學:數學
基本性質


矩陣轉置
套用
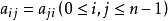




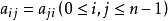

對稱矩陣(Symmetric Matrices)是指元素以主對角線為對稱軸對應相等的矩陣。線上性代數中,對稱矩陣是一個方形矩陣,其轉置矩陣和自身相等。1855年,埃米特(C.Hermite,...
如果有n階矩陣A,其矩陣的元素都為實數,且矩陣A的轉置等於其本身(aij=aji)(i,j為元素的腳標),則稱A為實對稱矩陣。...
設A為n維方陣,若有A'=-A,則稱矩陣A為反對稱矩陣。對於反對稱矩陣,它的主對角線上的元素全為零,而位於主對角線兩側對稱的元反號。反對稱矩陣具有很多良好的...
實反對稱矩陣(real antisymmetric matrix)是一種反對稱矩陣,指歐氏空間的反對稱變換在標準正交基下的矩陣,即元素aij都是實數,並且aij=-aji(i,j=1,2,…),n的...
矩陣是很多科學與工程計算問題中研究的數學對象,在實際套用中,經常出現一些階數很高的矩陣,同時在矩陣中有很多值相同的元素並且它們的分布有一定的規律——稱為特殊...
復反對稱矩陣是一種反對稱矩陣,指aij=-aji(i,j=1,2,...,n)的n階復矩陣A=(aij)。...... 復反對稱矩陣是一種反對稱矩陣,指aij=-aji(i,j=1,2,......
黑塞矩陣(Hessian Matrix),又譯作海森矩陣、海瑟矩陣、海塞矩陣等,是一個多元函式的二階偏導數構成的方陣,描述了函式的局部曲率。黑塞矩陣最早於19世紀由德國數學家...
厄米特矩陣(Hermitian Matrix,又譯作“埃爾米特矩陣”或“厄米矩陣”),指的是自共軛矩陣。矩陣中每一個第i行第j列的元素都與第j行第i列的元素的共軛相等。...
埃爾米特矩陣(又稱“自共軛矩陣”)是共軛對稱的方陣。埃爾米特矩陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等。n階複方陣A的對稱單元互...
對稱C矩陣(symmetric conference matrix)與阿達馬矩陣有關的一類矩陣,若元素為士1的n階對稱矩陣C的對角線元均為1且適合等式(C一1)2= <n一1>1,則稱C為對稱...
將矩陣的行列互換得到的新矩陣稱為轉置矩陣,轉置矩陣的行列式不變。...... 如果 ,則稱矩陣 為反對稱矩陣。 [1] 轉置矩陣運算性質 編輯 (1) ;(2) ;...
《實對稱矩陣的擬特徵值理論與套用》是新星出版社出版的圖書,作者是朱小平。該書主要介紹了實對稱矩陣的擬特徵值的分析方法及實際套用。...
對稱面有多個義項。一個是指群論在化學中的套用,一個是指結晶學名詞,還有一個是幾何學的對稱面。...
代數式包括有理式(整式,分式)和無理式。線上性代數中用矩陣(向量)代替代數式中的實數,得到的代數式稱為矩陣代數式。矩陣代數式遵守代數式的規律,同時具備特殊...
邏輯結構分為兩部分:V和E集合。因此,用一個一維數組存放圖中所有頂點數據;用一個二維數組存放頂點間關係(邊或弧)的數據,這個二維數組稱為鄰接矩陣。鄰接矩陣又分...
GRAM,格拉姆矩陣,以丹麥數學家約爾根·佩爾森·格拉姆命名。...... 內積空間中一族向量 格拉姆矩陣(Gramian matrix 或 Gram matrix, Gramian)是內積的對稱矩陣,其元...
所謂近似對稱矩陣是指矩陣中僅有極少一部分元素是非對稱的,在將對角線以上的非對稱元素用其對角線以下的對稱元素替代後,該矩陣就變成了一個對稱矩陣.在求解非線性...
旋轉矩陣(英語:Rotation matrix)是在乘以一個向量的時候有改變向量的方向但不改變大小的效果並保持了手性的矩陣。旋轉矩陣不包括點反演,點反演可以改變手性,也就是...
)=x'Ax與n階實對稱矩陣A=(aij)n×n是互相唯一確定的,稱A是二次型f的矩陣,稱f是以A為矩陣的二次型 [2] 。(2) 只有平方項 而沒有交叉項 ,i≠j的二...
