基本介紹
- 中文名:主對角線
- 外文名:leading diagonal
- 所屬學科:數學
- 相關概念:n階方陣、n階行列式、對角陣等
定義


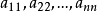
n階行列式的定義

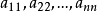
主對角線行列式

次對角線行列式

方陣對角化

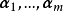

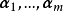












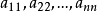

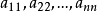



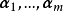

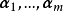









在一個n階方陣(或是n階行列式)中,從左上角到右下角這一斜線上的n 個元素的位置,叫做n 階方陣(或行列式)的主對角線。...
對角線,幾何學名詞,定義為連線多邊形任意兩個不相鄰頂點的線段,或者連線多面體任意兩個不在同一面上的頂點的線段。另外在代數學中,n階行列式,從左上至右下的數...
對角矩陣(diagonal matrix)是一個主對角線之外的元素皆為0的矩陣,常寫為diag(a1,a2,...,an) 。對角矩陣可以認為是矩陣中最簡單的一種,值得一提的是:對角線...
對角線法則是一種廣泛套用的法則,分為化學中的對角線法則、攝影中的對角線法則、數學中的對角線法則、四國軍旗的對角線法則...
只有對角線上有非0元素的矩陣稱為對角矩陣,或說若一個方陣除了主對角線上的元素外,其餘元素都等於零,則稱之為對角陣。...
對角矩陣是指只有主對角線上含有非零元素的矩陣,即,已知一個n×n矩陣 ,如果對於 ,則該矩陣為對角矩陣。如果存在一個矩陣 ,使 的結果為對角矩陣,則稱矩陣 將...
線上性代數中,三對角矩陣是矩陣的一種,它“幾乎”是一個對角矩陣。準確來說:一個三對角矩陣的非零係數在如下的三條對角線上:主對角線、低對角線、高對角線。...
對角優勢矩陣是一類特殊的方陣,複數域上的m×m矩陣A, 如果它的的第一行主對角線元素的模均不小於非主對角線元素模之和則稱A為對角優勢矩陣。 第i行非對角元素...
渠道對角線理論研究是對渠道權力轉移規律進行動態研究的一種新的嘗試: 研究表明,隨著時代的變化,渠道權力由初期的生產商擁有過渡到發展時期的中間商擁有,最終在步入...
在矩陣的乘法中,有一種矩陣起著特殊的作用,如同數的乘法中的1,這種矩陣被稱為單位矩陣。它是個方陣,從左上角到右下角的對角線(稱為主對角線)上的元素均為1...
三角矩陣是方形矩陣的一種,因其非零係數的排列呈三角形狀而得名。三角矩陣分上三角矩陣和下三角矩陣兩種。上三角矩陣的對角線左下方的係數全部為零,下三角矩陣的...
對稱矩陣(Symmetric Matrices)是指元素以主對角線為對稱軸對應相等的矩陣。線上性代數中,對稱矩陣是一個方形矩陣,其轉置矩陣和自身相等。1855年,埃米特(C.Hermite,...
行列式中若關於主對角線對稱的元素僅符號相反,即aij=-aji,則行列式叫做斜對稱行列式。對於n階斜對稱行列式d有關係式d=(一1)nd,從而可知奇數階的斜對稱行列式總是...
若矩陣A可對角化,則其對角矩陣Λ的主對角線元素全部為A的特徵值,其餘元素全部為0。(一個矩陣的對角陣不唯一,其特徵值可以換序,但都存在由對應特徵向量順序組成...
實際上,主子式的主對角線元素是原 n 階行列式的主對角線元素的一部分,且順序相同。值得注意的是,根據定義,i 階主子式是不唯一的,而 i 階順序主子式是唯一的...
函式功能:函式在FreeMat、Matlab中該函式用於構造一個對角矩陣(功能:在FreeMat、Matlab中該函式用於構造一個對角矩陣(不在對角線上元素全為0的方陣)或者以向量(在...
(7)存在主對角線元素全為正的實三角矩陣R,使A=R′R[2]。充要條件 (1)n 元實二次型 正定 它的正慣性指數為 n;(2) 一個實對稱矩陣 A 正定 A 與 E...
三階行列式直接計算——對角線法 標準方法是在已給行列式的右邊添加已給行列式的第一列、第二列。我們把行列式的左上角到右下角的對角線稱為主對角線,把右上角...
①對無向圖而言,鄰接矩陣一定是對稱的,而且主對角線一定為零(在此僅討論無向簡單圖),副對角線不一定為0,有向圖則不一定如此。...
布列安桑(Brianchon)定理是一個射影幾何中的著名定理,它斷言六條邊和一條圓錐曲線相切的六邊形的三條對角線共點,此點被稱為該六邊形的布列安桑點。...
