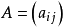斜對稱行列式

行列式中若關於主對角線對稱的元素僅符號相反，即a_ij=-a_ji，則行列式叫做斜對稱行列式。對於n階斜對稱行列式d有關係式d=(一1)ⁿd，從而可知奇數階的斜對稱行列式總是等於0。

基本介紹

• 中文名：斜對稱行列式
• 外文名：skew-symmetric determinant
• 所屬學科：數學
• 所屬問題：高等代數（行列式）

定義

斜對稱行列式(skew-symmetric determinant)是類似於斜對稱矩陣的一種特殊行列式。一個行列式，如果其主對角線上的元素全為零，而關於主對角線對稱位置上的元素絕對值相等符號相反，則稱為斜對稱行列式。方陣

或其行列式，當 時（因此 ），叫做斜對稱方陣或斜對稱行列式。例如

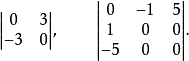
相關定理

定理1 方陣A為斜對稱的必要及充分條件為 。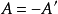

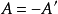
定理2 為斜對稱是在且僅在 為斜對稱時。

定理3 奇數次斜對稱方陣（或其行列式）的附屬方陣（或其行列式）為對稱的的，但偶數次斜對稱方陣（或其行列式）的附屬方陣（或其行列式）仍為斜對稱的。

定理4 滿秩斜對稱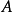方陣 的逆方陣 亦為斜對稱的。

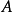
定理5 偶數次斜對稱行列式中主對角線上的元素的余因式均等於0。

定理6 奇數次斜對稱行列式恆等於零（或奇數次斜對稱方陣為降秩的）。

定理7 偶數次斜對稱行列式為其元素的某多項式的完全平方。

定理8 若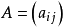 為n次降秩斜對稱方陣，則 。

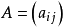
定理9若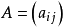 為奇數次斜對稱方陣時，則 。

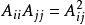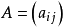
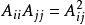
定理10若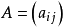 為偶數次斜對稱方陣時，則任何余因式 等於零。偶數次降秩斜對稱方陣的附屬附屬方陣為零方陣。