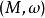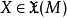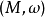辛向量場

在數學與物理學中，辛向量場（symplectic vector field）是流保持辛形式的向量場。

基本介紹

• 中文名：辛向量場
• 外文名：symplectic vector field
• 分類：數理科學

簡介

如果 是一個辛形式，則如果向量場 的流保持辛結構，則稱為一個辛向量場。換句話說，李導數為零：

或者，一個向量場是辛的如果它與辛形式內乘是閉的（內乘給出從向量場到1-形式的一個映射，因辛形式的非退化性這是一個同構）。兩個定義的等價性從辛形式的閉性與李導數用外導數表示的嘉當公式推出。

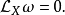
如果一個向量場與辛形式的內乘是恰當的（特別地是閉的），稱為哈密頓向量場。如果第一德拉姆上同調群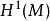 是平凡的，故所有閉形式是恰當的，所以辛相鄰場是哈密頓的。這就是說：“一個辛向量場是哈密頓的之阻礙屬於 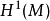。”特別地，單連通空間上的辛向量場是哈密頓的。

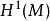
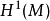
兩個辛向量場的李括弧是哈密頓的，從而辛向量集合與哈密頓向量場集合各自形成一個李代數。

辛形式

數學中，一個辛矢量空間是帶有辛形式ω 的向量空間V，所謂辛形式即一個非退化斜對稱的雙線性形式。

確切地說，一個辛形式是一個雙線性形式 ω ：V×V→R滿足：

• 斜對稱：ω(u,v) = −ω(v,u)，對所有u,v∈V成立；
  
• 非退化：如果 ω(u,v) = 0 對所有v∈V成立，那么u= 0 。
  

取定一組基，ω 能表示為一個矩陣。以上兩個條件表明這個矩陣必須是斜對稱非奇異矩陣。這不同於下面將介紹的辛矩陣，辛矩陣表示空間的一個辛變換。

如果V是有限維的那么維數必須為偶數，因為每個奇數階斜對稱矩陣的行列式為 0。

非退化斜對稱雙線性形式和非退化“對稱”雙線性形式，比如歐幾里得向量空間的內積，的表現非常不同。歐幾里得內積g，對任何非零向量v，均有g(v,v) > 0 成立；但是一個辛形式 ω 滿足 ω(v,v) = 0 。