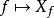在數學與物理中,哈密頓向量場是辛流形上一個向量場,定義在任何能量函式或哈密頓函式上。以物理學家和數學家威廉·盧雲·哈密頓命名。哈密頓向量場是經典力學中的哈密頓方程的幾何表現形式,哈密頓向量場的積分曲線表示哈密頓形式的運動方程的解。由哈密頓向量場生成的流是辛流形的微分同胚,在物理中稱為典範變換,在數學中稱為(哈密頓)辛同胚。
哈密頓向量場可以更一般地定義在任何泊松流形上。對應於流形上的函式 f 與 g 的兩個哈密頓向量場的李括弧也是一個哈密頓向量場,其哈密頓函式由 g 與 f 的泊松括弧給出。
基本介紹
- 中文名:哈密頓向量場
- 外文名:Hamiltonian vector field
- 學科:物理
定義



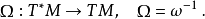


例子
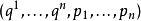



性質
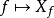


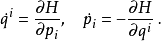
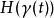



泊松括弧