向量微分運算元,Nabla運算元(nabla operator),又稱劈形運算元,倒三角運算元,是一個微分運算元。
基本介紹
介紹
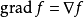
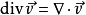

定義

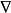

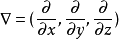


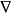
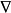
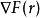

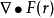
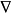


向量微分運算元,Nabla運算元(nabla operator),又稱劈形運算元,倒三角運算元,是一個微分運算元。
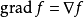
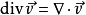


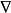

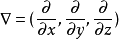


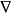
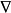
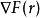

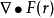
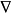

在磁場和電場理論中,為簡化運算,引入了一些運算元的符號,它們已經成為場論分析中不可缺少的工具,套用較多的有哈密頓運算元和拉普拉斯運算元。哈密頓運算元( Hamiltonian), ...
向量微分運算元,Nabla運算元(nabla operator),又稱劈形運算元,倒三角運算元,是一個微分運算元。...
Del運算元或稱Nabla運算元,在中文中也叫向量微分運算元、劈形運算元、倒三角運算元,是一個向量微分運算元,但本身並非一個向量。...
哈密頓算符哈密頓運算元 編輯 首先,“ ”這個東西具有“雙重性格”,它既是一個矢量,又是一個微分運算元(求導運算),所以哈密頓算符兼具矢量和微分的性質。按照定義:...
函式H被稱為哈密爾頓運算元或哈密爾頓能量函式。 然後將辛流形稱為相位空間。 哈密爾頓函式在辛流形上引入一個特殊的向量場,稱為哈密爾頓矢量場。 哈密頓函式在矩陣...
量子力學中,哈密頓算符(Hamiltonian) H為一個可觀測量(observable),對應於系統...注意到這些基態都假設與時間無關,因而我們可以也假設哈密頓運算元也獨立於時間。...
劈形運算元在標準HTML中寫為&nabla,而在LaTeX中為\nabla。在Unicode中,它是十進制數8711,也即十六進制數0x2207。劈形運算元在數學中用於指代梯度算符,並形成散度、...
通過與經典力學類似,哈密頓量通常表示為對應於系統的動能和勢能的運算符的總和。H=T+V(其中T是動能,V是勢能)。是動量運算元,其中∇是del運算符。 ∇自身的點...
哈密頓向量場泊松括弧 編輯 哈密頓向量場的概念導致了辛流形M上的可微函式的一個斜對稱雙線性運算元,這就是泊松括弧,由如下公式定義...
威廉·哈密頓爵士(Sir William Rowan Hamilton,1805年8月4日-1865年9月2日),...哈密頓函式既是一個經典物理學中的函式,也是量子物理學中的一個運算元, 還是圖論...
這些系統包括達芬方程、一維p-Laplacian方程、二階哈密頓系統、一階哈密頓系統及其自伴運算元方程等。與法國數學家Ekeland的名著ConvexitymethodsinHamiltonianmechanics及其...
哈特里根據他的假設,將體系電子哈密頓運算元分解為若干個單電子哈密頓運算元的簡單代數和,每個單電子哈密頓運算元中只包含一個電子的坐標,因而體系多電子波函式可以表示為...
向量分析研究定義在標量場或向量場定義的不同微分運算元,通常用的向量運算元(∇)來表示,也被稱為“Nabla運算元”。向量分析的五個最重要的微分運算 [2] :...
劈形算符在標準HTML中寫為∇ 而在LaTeX中為\nabla。在Unicode中,它是十進制數8711,也即十六進制數0x2207。詞條標籤: 數學, 學科 ...
當李群是由一個哈密頓量定義的,它稱為一個“由能量量子化”。從李代數到連續線性運算元李代數對應的運算元通常也稱為量子化;這是物理學中更常見的方式。參見外爾...
