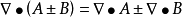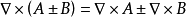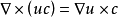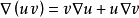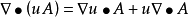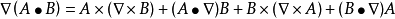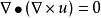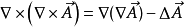在磁場和電場理論中，為簡化運算，引入了一些運算元的符號，它們已經成為場論分析中不可缺少的工具，套用較多的有哈密頓運算元和拉普拉斯運算元。哈密頓運算元（ Hamiltonian）， 數學符號為▽，讀作 del ta或nabla。量子力學中，哈密頓運算元(Hamiltonian) 為一個可觀測量（observable），對應於系統的的總能量。
基本介紹
- 中文名：哈密頓運算元
- 外文名：Hamiltonian
- 數學符號：▽
- 讀作：delta 或 nabla
- 縮寫符號：H
- 套用學科：磁場和電場理論，數學
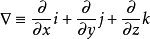
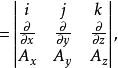
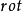
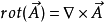
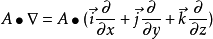
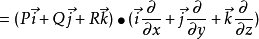
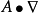
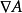
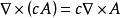
定義,運算規則,矢性微分運算元,與梯度、散度、旋度的關係,與拉普拉斯運算元的關係,常用公式,準備工作,公式匯總,
定義
哈密頓（W.R.Hamiltonian）引進了一個矢性微分運算元：
，稱之為哈密頓運算元或者▽ 運算元。
記號▽ 讀作“那勃樂（Nabla）”，在運算中既有微分又有矢量的雙重運算性質，其優點在於可以把對矢量函式的微分運算轉變為矢量代數的運算，從而可以簡化運算過程，並且推導簡明扼要，易於掌握。
▽ 本身並無意義，就是一個運算元，同時又被看作是一個矢量，在運算時，具有矢量和微分的雙重身份。
運算規則
矢性微分運算元
哈密頓引進了一個矢性微分運算元稱為哈密頓運算元或
運算元：
。
記號讀作“那勃勒”，在運算中既有微分又有失量的雙重運算性質，其優點在於可以把對矢量函式的微分運算轉變為矢量代數的運算，從而可以簡化運算過程，並且推導簡明扼要，易於掌握。
其運算規則為
前面見過的梯度、散度和旋度都可以用運算元表示為
與梯度、散度、旋度的關係
（1）
；
（2）
；
（3）
。
與拉普拉斯運算元的關係
常用公式
準備工作
它既可以作用在數性函式 u=u(M) 上，又可以作用在矢性函式B(M) 上。
（1）
；
（2）
。
需要注意的是：
（1）
與
是完全不同的；
（2）
與
是無意義的。
公式匯總
（1）
；
（2）
；
（3）
；
（4）
；
（5）
；
（6）
；
（7）
；
（8）
；
（9）
；
（10）
；
（11）
；
（12）
；
（13）
；
（14）
；
（15）
；
（16）
；
（17）；
（18），其中。
