基本介紹
- 中文名:哈密頓算符
- 外文名:Hamiltonian
- 套用:系統的的總能量
- 組成:純點、絕對連續、奇點
- 符號:H
- 領域:物理、量子力學
簡介


算法





哈密頓運算元

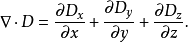









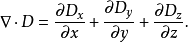
量子力學中,哈密頓算符(Hamiltonian) H為一個可觀測量(observable),對應於系統的的總能量。一如其他所有算符,哈密頓算符的譜為測量系統總能時所有可能結果的集合...
在磁場和電場理論中,為簡化運算,引入了一些運算元的符號,它們已經成為場論分析中不可缺少的工具,套用較多的有哈密頓運算元和拉普拉斯運算元。哈密頓運算元( Hamiltonian), ...
量子力學中,哈密頓算符(Hamiltonian) H為一個可觀測量(observable),對應於系統的的總能量。一如其他所有算符,哈密頓算符的譜為測量系統總能時所有可能結果的集合...
哈密頓量是一個物理辭彙,是系統的能量算符,是一個描述系統總能量的算符,以H表示。哈密頓量在大部分的量子理論公式中十分重要。...
哈密頓(William Rowan Hamilton 1805~1865) 英國數學家,物理學家,力學家。1805年8月4日生於愛爾蘭都柏林;1865年9月2日卒於愛爾蘭都柏林。...
物理學中,特別是量子物理常常使用到算符的概念。如動量算符、角動量算符、哈密頓算符、拉格朗日算符等等。下面主要介紹量子物理算符的一些概念:...
當一個粒子在保守力場中運動時,它的勢能與時間無關,此時,體系的能量算符定義為動能算符和勢能算符之和。在保守力場中,體系的能量算符也就是該體系的哈密頓算...
(2)哈密頓算符與角動量算符之間的對易關係思考哈密頓算符 與 的交換算符,,與 是對易的, 與 彼此是相容可觀察量,兩個算符擁有共同的本徵態。根據不確定性...
量子力學中的力學量和算符 又如,在勢為(r)的力場中運動的粒子能量算符(也稱哈密頓算符)為 量子力學中的力學量和算符 詞條圖冊 更多圖冊 ...
哈密頓函式簡介 編輯 可以使用“symplectic manifold”的任何平滑的實值函式H來定義哈密爾頓函式。 函式H被稱為哈密爾頓運算元或哈密爾頓能量函式。 然後將“symplectic ...
算符 定義 一個函式空間到函式空間上的映射 套用領域 數理科學 目錄...常見的運算元有微分運算元,梯度運算元,散度運算元,拉普拉斯運算元,哈密頓運算元等。 [2] ...
庫侖算符是以夏爾·奧古斯丁·庫侖的名字命名的,是一個在量子化學領域中經常使用...量子算符將某量子態映射為另一種量子態。庫侖算符參見 編輯 哈密頓算符 交換...
安德森模型是一種哈密頓算符,通常用來描述重費米子。...... 安德森模型是一種哈密頓算符,通常用來描述重費米子,是由菲利普·安德森發展出來的理論。以數學的方法...
H為哈密頓算符。這個方程在這個形式下充分顯示出了時間與空間的對應性(時間與能量相對應,正如空間與動量相對應,後述)。這種算符(物理量)不隨時間變化而狀態隨...
薛丁格方程為其中,H是表征波函式總能量的哈密頓算符, 是物理系統的波函式,i是虛數。h是約化普朗克常數。將波函式歸一化為。則薛丁格方程成為...
在量子力學裡,埃倫費斯特定理(Ehrenfest theorem)表明,量子算符的期望值對於時間的導數,跟這量子算符與哈密頓算符的對易算符相關。...
,總可以得到另一組等價滿足此特定哈密頓算符的波函式。相比原先的波函式,乘上此相位對布洛赫態的性質不產生影響,但其對應的瓦尼爾函式會因此發生改變。藉助...
海特勒-倫敦方法處理氫分子 氫分子的哈密頓算符是: 式中rA1、rB1為核A、B與電子1之間的距離;r12為兩個電子之間的距離;RAB為兩個原子核之間的距離……(圖1)...
對應於代表該量的算符對其波函式的作用;波函式的模平方代表作為其變數的物理...,En是能量本徵值,H是哈密頓運算元。於是經典物理量的量子化問題就歸結為薛丁格波動...
倒三角形為哈密頓運算元。注意:(1)在不同的慣性參照系中,麥克斯韋方程組有同樣...以“力”作為基本的研究對象,在數學上引入了有別於經典數學的矢量偏微分運算符...
