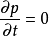埃倫費斯特定理

在量子力學里，埃倫費斯特定理（Ehrenfest theorem）表明，量子算符的期望值對於時間的導數，跟這量子算符與哈密頓算符的對易算符相關。

基本介紹

• 中文名：埃倫費斯特定理
• 外文名：Ehrenfest theorem
• 提出者：保羅·埃倫費斯特
• 套用學科：物理學
• 適用領域範圍：量子力學

簡介

量子算符的期望值對於時間的導數，跟這量子算符與哈密頓算符的對易算符，兩者之間的關係，以方程表達為：

其中，A是某個量子算符，<A>是它的期望值，H是哈密頓算符，t是時間，ℏ是約化普朗克常數。

埃倫費斯特定理是因物理學家保羅·埃倫費斯特命名。在量子力學的海森堡繪景里，埃倫費斯特定理非常顯而易見；取海森堡方程的期望值，就可以得到埃倫費斯特定理。埃倫費斯特定理與哈密頓力學的劉維爾定理密切相關；劉維爾定理使用的泊松括弧，對應於埃倫費斯特定理的對易算符。實際上，從根據經驗法則，將對易算符換為泊松括弧乘以 ，再取趨向於0的極限，含有對易算符的量子定理就可以改變為含有泊松括弧的經典定理。

導引

假設，一個物理系統的量子態為 ，則算符A的期望值對於時間的導數為

薛丁格方程表明哈密頓算符H與時間t的關係為

其共軛複數為

因為哈密頓算符是厄米算符， 。所以，

將這三個方程代入 的方程，則可得到

所以，埃倫費斯特定理成立：

實例

使用埃倫費斯特定理，可以簡易地證明，假若一個物理系統的哈密頓量顯性地不含時間，則這系統是保守系統。

從埃倫費斯特定理，可以計算任何算符的期望值對於時間的導數。特別而言，速度的期望值和加速度的期望值。知道這些資料，就可以分析量子系統的運動行為。

保守哈密頓量

思考哈密頓算符H：

假若，哈密頓量顯性地不含時間， ，則

哈密頓量是個常數 。

位置期望值與時間

試想一個質量為m的粒子，移動於一維空間．其哈密頓量是

其中，x為位置，p是動量，V是位勢。

套用埃倫費斯特定理，

由於 ，位置的期望值對於時間的導數等於速度的期望值：

這樣，可以得到動量p的期望值。

動量期望值與時間

套用埃倫費斯特定理，

由於p與自己互相交換，所以， 。又在坐標空間裡，動量算符不含時間： 。所以，

將泊松括弧展開，

使用乘法定則，

在量子力學裡，動量的期望值對於時間的導數，等於作用力F的期望值。