基本介紹
- 中文名:共軛複數
- 外文名:conjugate complex number
- 類別:定律
- 類型 :概念
- 學科:數學
- 套用:初等幾何問題
公式

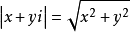
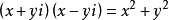
代數特徵


加法法則
減法法則
乘法法則
除法法則
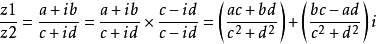
開方法則
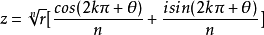
共軛法則
運算特徵




模的運算性質





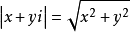
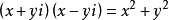


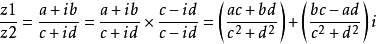
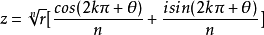







共軛複數,兩個實部相等,虛部互為相反數的複數互為共軛複數(conjugate complex number)。當虛部不為零時,共軛複數就是實部相等,虛部相反,如果虛部為零,其共軛複數...
共軛在數學、物理、化學、地理等學科中都有出現。 本意:兩頭牛背上的架子稱為軛,軛使兩頭牛同步行走。共軛即為按一定的規律相配的一對。通俗點說就是孿生。在...
兩個複數如x+iy和x-iy,其實部和虛部數值分別相等,但虛部符號相反,則稱這兩個複數為共軛數。在阿爾崗圖上可以認為它們是以實軸互為鏡面對稱。...
我們把形如z=a+bi(a,b均為實數)的數稱為複數,其中a稱為實部,b稱為虛部,i稱為虛數單位。當z的虛部等於零時,常稱z為實數;當z的虛部不等於零時,實部...
複數運算法則有:加減法、乘除法。兩個複數的和依然是複數,它的實部是原來兩個複數實部的和,它的虛部是原來兩個虛部的和。複數的加法滿足交換律和結合律。此外,...
一元二次方程,若用公式法解得根(即)判別式小於零,則該方程的根為2個共軛復根。因為負數在開平方時存在+i和-i,所以如果有複數根則必是共軛的...
共軛阻抗是指一對阻抗,它們的實部分量(阻)相等,虛部分量(抗)大小相等而符號相反。共軛阻抗可用共軛複數來表示。...
若(a1,a2,a3)為一個元素(點或直線)的齊次坐標,則由ai的共軛複數所成坐標構成的另一個同類元素為其共軛復元素,其主要結論有:1.一元素為實元素充分必要條件是...
對於複數z=x+iy,其中x,y是任意實數,y稱為複數z的虛部。y=Im z。在笛卡爾直角坐標系中,y軸的值為虛部。利用實部和虛部可以判斷兩個複數是否相等,定義共軛...
共軛複數a+bi=a-bi-(z1+z2)=_z1+_z2-(z1-z2)=_z1-_z2-(z1z2)=_z1_z2-(zn)=(_z)n-z1/z2=_z1/_z2...
有兩個不同的解,它們都是有效的,且互為共軛複數。更加確切地,一旦固定了方程的一個解i,那么−i(不等於i)也是一個解,由於這個方程是唯一的定義,因此這個定義...
