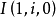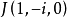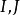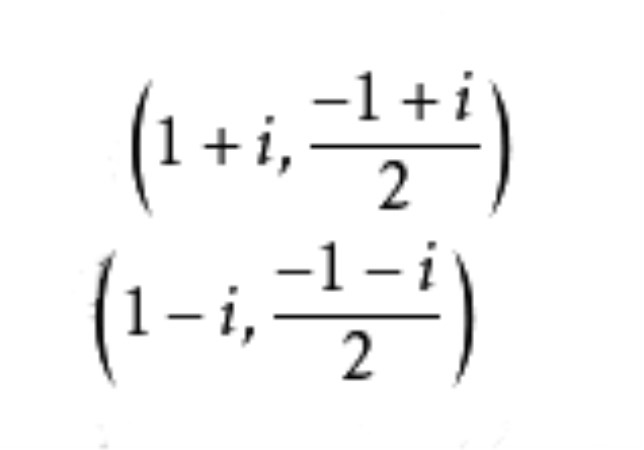二維共軛復元素

若(a₁，a₂，a₃)為一個元素(點或直線)的齊次坐標，則由a_i的共軛複數所成坐標構成的另一個同類元素為其共軛復元素，其主要結論有：1．一元素為實元素充分必要條件是該元素與其共軛復元素重合；2．若點x在直線u上，則x的共軛復點在u的共軛直線上；3．兩共軛虛直線的交點為實點，兩共軛虛點的連線為實直線；4．在一虛直線上有唯一實點，過一虛點有唯一一條實直線。

基本介紹

• 中文名：二維共軛復元素
• 外文名：two-dimensional conjugate complex elements
• 所屬學科：數學
• 所屬問題：高等幾何(射影幾何)
• 相關概念：復二維空間、共軛

基本介紹

二維共軛復元素是復二維空間中坐標互相共軛的兩個元素，若(a₁，a₂，a₃)為一個元素(點或直線)的齊次坐標，取a₁，a₂，a₃的共軛複數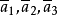 ，則 為另一個同類元素(點或直線)的齊次坐標，此二元素稱為二維共軛復元素(two-dimensionalconjugate complex elements)。因為齊次坐標允許差一個非零常數因子，所以兩個第三坐標不是零的元素為共軛復元素時，必須且只須其對應的非齊次坐標為共軛複數，但兩個共軛復元素的對應齊次坐標不一定為共軛複數。例如，(1-i，i，1)與(-1-i，i，-1)為兩個共軛復點的齊次坐標，這是由於其非齊次坐標分別是(1-i，i)和(1+i，-i)。

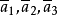
定理及推論

定理1 一元素為實元素的充要條件為該元素與其共軛復元素重合。

定理2 如果點x在直線u上，則x的共軛復點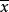 在u的共軛復直線u上。

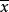
定理3 兩共軛虛直線的交點為一實點，兩共輻虛點的連線為一實直線。

推論 在一虛直線上有唯一一個實點，通過一虛點有唯一一條實直線。

例題解析

例1 證明：(2，i，1-i)與(2+2i，1-i，2i)表示一對共軛復點，並求其連線方程。

證： 點(2，i，1-i)之非齊次坐標為 ，

點(2+2i，1-i，2i)之非齊次坐標為 。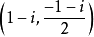

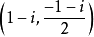
顯然其坐標為共軛複數，所以此二點為共軛復點。其連線方程為：

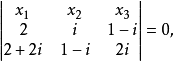
即： 。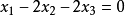

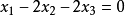
例2 (1)求過(1，i，0)之實直線；

(2)求直線[2，i，3-4i]上之實點。

解： (1)通過點(1，i，0)之實直線必過其共軛復點(1，-i，0)，故所求為 ；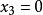

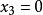
(2)直線[2，i，3-4i]上之實點為它與共軛復直線[2，-i，3+4i]之交點，故所求為點(-3，8，2)。

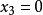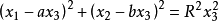例3 求無窮遠直線 與圓 的交點。

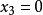
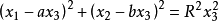
解：解聯立方程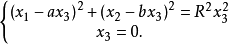

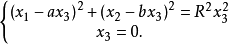
得交點為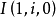和。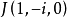

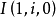
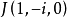
注意 平面上一圓必經過兩個共軛復點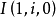和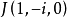，反之，一實二次曲線如果經過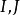二點，則必為圓。