公式 三角函式
sin(a+bi)=sin(a)cos(bi)+sin(bi)cos(a)
=sin(a)cosh(b)+isinh(b)cos(a)
cos(a-bi)=cos(a)cos(bi)+sin(bi)sin(a)
=cos(a)cosh(b)+isinh(b)sin(a)
tan(a+bi)=sin(a+bi)/cos(a+bi)
cot(a+bi)=cos(a+bi)/sin(a+bi)
sec(a+bi)=1/cos(a+bi)
csc(a+bi)=1/sin(a+bi)
四則運算
(a+bi)±(c+di)=(a±c)+(b±d)i
(a+bi)(c+di)=(ac-bd)+(ad+bc)i
(a+bi)/(c+di)=(ac+bd)/(c2 +d2 )+(bc-ad)i/(c2 +d2 )
r1(isina+cosa)r2(isinb+cosb)=r1r2[cos(a+b)+isin(a+b)]
r1(isina+cosa)/r2(isinb+cosb)=r1/r2[cos(a-b)+isin(a-b)]
r(isina+cosa)
n =
(isinna+cosna)
共軛複數
a+bi=a-bi
-(z1 +z2 )=_z1 +_z2
-(z1 -z2 )=_z1 -_z2
-(z1 z2 )=_z1 _z2
-(zn )=(_z)n
-z1 /z2 =_z1 /_z2
-zz =|z|2 ∈R
乘方
zm · zn =zm+n
zm /zn =zm-n
(zm )n =zmn
z1 m · z2 m =(z1 z2 )m
(zm )1/n =zm/n
z· z· z…· z(n個)=zn
z1 n =z2 -->z1=z2 1/n
ln(a+bi)=ln(a^2+b^2)/2+i Arctan(b/a)
logai(x)=ln(x)/[ iπ/2+ lna]
xai+b =xai · xb =eialn(x) · xb =xb [cos(alnx) + i sin(alnx). ]
定義 在數學裡,將偶指數冪是
負數 的數定義為
純虛數 。所有的虛數都是
複數 。定義為i
2 =-1。但是虛數是沒有算術根這一說的,所以±√(-1)=±i。對於z=a+bi,也可以表示為e的iA次方的形式,其中e是常數,i為虛數單位,A為虛數的幅角,即可表示為z=cosA+isinA。
實數 和虛數組成的一對數在複數範圍內看成一個數,起名為複數。虛數沒有正負可言。不是實數的複數,即使是純虛數,也不能比較大小。
起源 要追溯虛數出現的軌跡,就要聯繫與它相對實數的出現過程。我們知道,實數是與虛數相對應的,它包括有理數和
無理數 ,也就是說它是實實在在存在的數。
無理數的發現,應該歸功於古希臘
畢達哥拉斯學派 。無理數的出現,與德謨克利特的“
原子論 ”發生矛盾。根據這一理論,任何兩個
線段 的比,不過是它們所含原子數目的經。而
勾股定理 卻說明了存在著不可通約的線段。
實軸和虛軸 不可通約線段的存在,使古希臘的數學家感到左右為難,因為他們的學說中只有整數和分數的概念,他們不能完全表示正方形對角線與邊長的比,也就是說,在他們那裡,正方形對角線與邊長的比不能用任何“數”來表示。西亞他們已經發現了無理數這個問題,但是卻又讓它從自己的身邊悄悄溜走了,甚至到了希臘最偉大的代數學家
丟番圖 那裡,方程的無理數解仍然被稱為是“不可能的”。
“虛數”這個名詞是17世紀著名數學家、哲學家
笛卡爾 創製,因為當時的觀念認為這是真實不存在的數字。後來發現虛數可對應平面上的縱軸,與對應平面上橫軸的實數同樣真實。
人們發現即使使用全部的有理數和
無理數 ,也不能解決代數方程的求解問題。像x
2 +1=0這樣最簡單的
二次方程 ,在實數範圍內沒有解。12世紀的印度大數學家婆什伽羅都認為這個
方程 是沒有解的。他認為
正數 的平方是正數,
負數 的平方也是正數,因此,一個正數的
平方根 是兩重的;一個正數和一個負數,負數沒有平方根,因此負數不是
平方數 。這等於不承認方程的負數平方根的存在。
到了16世紀,義大利數學家
卡爾達諾 在其著作《大術》(《數學大典》)中,把記為1545R15-15m這是最早的虛數記號。但他認為這僅僅是個形式表示而已。1637年法國數學家笛卡爾,在其《幾何學》中第一次給出“虛數”的名稱,並和“實數”相對應。
1545年義大利米蘭的卡爾達諾發表了
文藝復興時期 最重要的一部代數學著作,提出了一種求解一般三次方程的求解公式:
形如:x3 +ax+b=0的三次方程解如下:
x={(-b/2)+[(b2 )/4+(a3 )/27]1/2 }1/3 +{(-b/2)-[(b2 )/4+(a3 )/27]1/2 }1/3
當卡丹試圖用該公式解方程x3 -15x-4=0時他的解是:x=[2+(-121)^(1/2)]^(1/3)+[2-(-121)^(1/2)]^(1/3)
在那個年代負數本身就是令人懷疑的,負數的平方根就更加荒謬了。因此卡丹的公式給出x=(2+j)+(2-j)=4。容易證明x=4確實是原方程的根,但卡丹不曾熱心解釋(-121)1/2 的出現。認為是“不可捉摸而無用的東西”。
直到19世紀初,高斯系統地使用了i這個符號,並主張用數偶(a、b)來表示a+bi,稱為複數,虛數才逐步得以通行。
虛數闖進數的領域時,人們對它的實際用處一無所知,在實際生活中似乎沒有用複數來表達的量,因此在很長一段時間裡,人們對它產生過種種懷疑和誤解。笛卡爾稱“虛數”的本意就是指它是虛假的;萊布尼茲則認為:“虛數是美妙而奇異的神靈隱蔽所,它幾乎是既存在又不存在的兩棲物。”歐拉儘管在許多地方用了虛數,但又說:“一切形如,√-1,√-2的數學式子都是不可能有的,想像的數,因為它們所表示的是
負數 的平方根。對於這
類數 ,我們只能斷言,它們既不是什麼都不是,也不比什麼都不是多些什麼,更不比什麼都不是少些什麼,它們純屬虛幻。”
繼歐拉之後,挪威測量學家維塞爾提出把複數(a+bi)用平面上的點來表示。後來高斯又提出了
複平面 的概念,終於使複數有了立足之地,也為複數的套用開闢了道路。現 在,複數一般用來表示
向量 (有方向的量),這在水利學、地圖學、航空學中的套用十分廣泛,虛數越來越顯示出其豐富的內容。
1843年,威廉·羅文·漢密爾頓(William Rowan Hamilton)將平面中的虛數軸的概念擴展到四元數想像的四維空間,其中三個維與複數域中的虛數相似。
隨著多項式環的商環的發展,假想數的概念變得更加顯著,但是也可以找到其他虛數,例如具有+1的平方的tessarines的j。 這個想法首先出現在1848年開始的James Cockle的文章中。
符號 1777年瑞士數學家
歐拉 (Euler,或譯為歐勒)開始使用符號
i 表示虛數的單位。而後人將虛數和實數有機地結合起來,寫成
a+bi 形式 (
a、b 為實數,
a 等於0時叫純虛數,ab都不等於0時叫複數,
b 等於0時就是實數)。
而在工程運算中,為了不與其他符號(如電流的符號)相混淆,有時也用j或k等字母來表示虛數的單位。
通常,我們用符號C來表示複數集,用符號R來表示實數集。
實際意義 我們可以在
平面直角坐標系 中畫出虛數系統。如果利用
橫軸 表示
全體實數 ,那么縱軸即可表示虛數。整個平面上每一點對應著一個複數,稱為
複平面 。橫軸和
縱軸 也改稱為實軸和虛軸。在此時,一點P坐標為P (a,bi),將坐標乘上i即點繞圓心逆時針旋轉90度。
虛數 不能滿足於上述圖像解釋的同學或學者可參考以下題目和說明:
若存在一個數,它的倒數等於它的相反數(或者它的倒數的相反數為其自身),這個數是什麼形式?
根據這一要求,可以給出如下方程:
-x = (1/x)
不難得知,這個方程的解x=±i (虛數單位)
由此,若有代數式 t'=ti,我們將i理解為從t的單位到t'的單位之間的轉換單位,則t'=ti將被理解為
-t' = 1/t
即
t' = - 1/t
這一表達式在幾何空間上的意義不大,但若配合
狹義相對論 ,在時間上理解,則可以解釋若相對運動速度可以大於光速c,相對時間間隔產生的虛數值,實質上是其實數值的負倒數。也就是所謂回到過去的時間間隔數值可以由此計算出來。
虛數成為微晶片和數字壓縮算法設計中的核心工具,虛數是引發電子學革命的量子力學的理論基礎。
虛數是用來表示事物中無法構成抽象概念的因素的抽象概念。
i的性質 i 的高次方會不斷作以下的循環:
i1 = i,
i2 = - 1,
i3 = - i,
i4 = 1,
i5 = i,
i6 = - 1.
...
in 具有周期性,且最小正周期是4.
∴ i4n =1,
i4n+1 =i,
i4n+2 =-1,
i4n+3 =-i.
由於虛數特殊的運算規則,出現了符號i
當ω=-1/2+(√3)/2i或ω=-1/2-(√3)/2i時:
ω2 + ω + 1 = 0
ω3 = 1
有關運算 許多實數的運算都可以推廣到i,例如指數、對數和
三角函式 。
一個數的ni次方為:
xni = cos(ln(xn )) + i sin(ln(xn )).
一個數的ni次方根為:
x1/ni = cos(ln(x1/n )) - i sin(ln((x1/n )).
以i為底的對數為:
log_i(x) = 2 ln(x)/ iπ.
i的餘弦是一個實數:
cos(i) = cosh(1) = (e + 1/e)/2 = (e2 + 1) /2e = 1.54308064.
sin(i) = sinh(1) i =[(e - 1/e)/ 2]i = 1.17520119 i.
i,e,π,0和1的奇妙關係:
eiπ +1=0
ii =e-π/2
相關描述 虛數 原作:勞倫斯·馬克·萊瑟(阿姆斯特朗大西洋州立學院)
翻譯:徐國強
虛文自古向空構,艾字如今可倍乘。所問逢人驚詫甚,生活何處有真能?嗟哉小試調音放,訝矣大為掌夜燈。三極體中知用否,交流電路肯鹹恆。憑君漫問荒唐義,負值求根疑竇增。情類當初聽慣耳,事關負數見折肱。幾分繁複融學域,百計聯席悅有朋。但看幾何三角地,蓬勃艾草意同承[①]。
IMAGINARY by Lawrence Mark LesserArmstrong Atlantic State University
Imaginary numbers, multiples of iEverybody wonders, "are they used in real life?"Well, try the amplifier I'm using right now -- A.C.!You say it's absurd,this root of minus one.but the same things once were heardAbout the number negative one!Imaginary numbers are a bit complex,But in real mathematics, everything connects:Geometry, trig and call all see "i to i."
[①] see "i to i."指可見
虛數符號 的套用,並諧音雙關see eye to eye 為意見一致引起了爭議
表達式 a=a+i
含義為與一切事物皆無
聯繫 的
概念 ,無論a任何變化,i都不會變。
實際意義 一切事物的值都可表示為:a+bi,而不是單有實數。

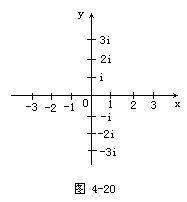 實軸和虛軸
實軸和虛軸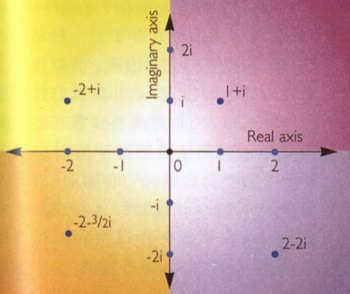 虛數
虛數

 實軸和虛軸
實軸和虛軸 虛數
虛數