簡介
薛丁格方程是
量子力學的基本方程。是1926年奧地利理論物理學家
薛丁格提出的。它描述微觀粒子的狀態隨時間變化的規律。微觀系統的狀態由波函式來描寫,薛丁格方程即是波函式的微分方程。若給定了初始條件和邊界的條件,就可由此方程解出
波函式。
方程定義
薛丁格方程(Schrodinger equation)在
量子力學中,體系的狀態不能用力學量(例如x)的值來確定,而是要用力學量的函式Ψ(x,t),即
波函式(又稱
機率幅,
態函式)來確定,因此波函式成為量子力學研究的主要對象。力學量取值的機率分布如何,這個分布隨時間如何變化,這些問題都可以通過求解波函式的薛丁格方程得到解答。這個方程是奧地利物理學家薛丁格於1926年提出的,它是量子力學最基本的方程之一,在量子力學中的地位與
牛頓方程在
經典力學中的地位相當,超弦理論試圖統一兩種理論。
薛丁格方程是量子力學最基本的方程,亦是量子力學的一個基本假定,其正確性只能靠實驗來確定。
量子力學中求解粒子問題常歸結為解薛丁格方程或定態薛丁格方程。薛丁格方程廣泛地用於
原子物理、
核物理和固體物理,對於原子、分子、核、固體等一系列問題中求解的結果都與實際符合得很好。
 薛丁格方程
薛丁格方程薛丁格方程僅適用於速度不太大的非相對論粒子,其中也沒有包含關於粒子
自旋的描述。當涉及相對論效應時,薛丁格方程由相對論量子力學方程所取代,其中自然包含了
粒子的自旋。
.薛丁格提出的量子力學基本方程 。建立於 1926年。它是一個非相對論的
波動方程。它反映了描述微觀粒子的狀態隨時間變化的規律,它在量子力學中的地位相當於牛頓定律對於經典力學一樣,是量子力學的基本假設之一。設描述微觀粒子狀態的波函式為Ψ(r,t),質量為m的微觀粒子在勢場V(r,t)中運動的薛丁格方程。在給定初始條件和邊界條件以及波函式所滿足的
單值、有限、連續的條件下,可解出波函式Ψ(r,t)。由此可計算粒子的分布
機率和任何可能實驗的平均值(
期望值)。當
勢函式V不依賴於時間t時,粒子具有確定的能量,粒子的狀態稱為
定態。定態時的波函式可寫成式中Ψ(r)稱為
定態波函式,滿足定態薛丁格方程,這一方程在數學上稱為
本徵方程,式中E為本徵值,它是定態能量,Ψ(r)又稱為屬於本徵值E的
本徵函式。
薛丁格方程是量子力學的基本方程,它揭示了微觀物理世界物質運動的基本規律,如牛頓定律在經典力學中所起的作用一樣,它是原子物理學中處理一切非相對論問題的有力工具,在
原子、分子、固體物理、
核物理、化學等領域中被廣泛套用。
背景與發展
1900年,
馬克斯·普朗克在研究
黑體輻射中作出將電磁輻射能量量子化的假設,因此發現將能量與頻率關聯在一起的普朗克關係式。1905年,
阿爾伯特·愛因斯坦從對於光電效應的研究又給予這關係式嶄新的詮釋:頻率為ν的
光子擁有的能量為hν;其中,因子h是
普朗克常數。這一點子成為後來
波粒二象性概念的早期路標之一。由於在
狹義相對論里,能量與動量的關聯方式類似頻率與波數的關聯方式,因此可以揣測,光子的動量與波長成反比,與波數成正比,以方程來表示這關係式。
路易·德布羅意認為,不單光子遵守這關係式,所有粒子都遵守這關係式。他於1924年進一步提出的
德布羅意假說表明,每一種微觀粒子都具有波動性與粒子性,這性質稱為波粒二象性。電子也不例外的具有這種性質。電子是一種
物質波,稱為“電子波”。電子的能量與動量分別決定了伴隨它的物質波所具有的頻率與波數。在原子裡,束縛電子形成
駐波;這意味著他的旋轉頻率只能呈某些離散數值。這些量子化軌道對應於離散
能級。從這些點子,德布羅意複製出
玻爾模型的能級。
在1925年,瑞士
蘇黎世每兩周會舉辦一場物理學術研討會。有一次,主辦者
彼得·德拜邀請薛丁格講述關於德布羅意的波粒二象性博士論文。那段時期,薛丁格正在研究氣體理論,他從閱讀愛因斯坦關於
玻色-愛因斯坦統計的論述中,接觸德布羅意的博士論文,在這方面有很精深的理解。在研討會裡,他將波粒二象性闡述的淋漓盡致,大家都聽的津津有味。德拜指出,既然粒子具有波動性,應該有一種能夠正確描述這種量子性質的
波動方程。他的意見給予薛丁格極大的啟發與鼓舞,他開始尋找這波動方程。檢試此方程最簡單與基本的方法就是,用此方程來描述氫原子內部束縛電子的物理行為,而必能複製出
玻爾模型的理論結果,另外,這方程還必須能解釋索末菲模型給出的精細結構。
很快,薛丁格就通過德布羅意論文的相對論性理論,推導出一個相對論性波動方程,他將這方程套用於
氫原子,計算出束縛電子的波函式。因為薛丁格沒有將電子的
自旋納入考量,所以從這方程推導出的精細結構公式不符合索末菲模型。他只好將這方程加以修改,除去相對論性部分,並用剩下的非相對論性方程來計算氫原子的
譜線。解析這微分方程的工作相當困難,在其好朋友數學家
赫爾曼·外爾鼎力相助下,他複製出了與玻爾模型完全相同的答案。因此,他決定暫且不發表相對論性部分,只把非相對論性波動方程與氫原子光譜分析結果,寫為一篇論文。1926年,他正式發表了這論文。
這篇論文迅速在量子學術界引起震撼。普朗克表示“他已閱讀完畢整篇論文,就像被一個迷語困惑多時,渴慕知道答案的孩童,現在終於聽到了解答”。愛因斯坦稱讚,這著作的靈感如同泉水般源自一位真正的天才。愛因斯坦覺得,薛丁格已做出決定性貢獻。由於薛丁格所創建的波動力學涉及到眾所熟悉的波動概念與數學,而不是
矩陣力學中既抽象又陌生的矩陣代數,量子學者都很樂意地開始學習與套用波動力學。自旋的發現者喬治·烏倫貝克驚嘆,“薛丁格方程給我們帶來極大的解救!”
沃爾夫岡·泡利認為,這論文應可算是最重要的著作之一。
薛丁格給出的薛丁格方程能夠正確地描述波函式的量子行為。在那時,物理學者尚不清楚如何詮釋波函式,薛丁格試圖以
電荷密度來詮釋波函式的絕對值平方,可並不成功。1926年,玻恩提出
機率幅的概念,成功地詮釋了波函式的物理意義。但是薛丁格與愛因斯坦觀點相同,都不贊同這種統計或機率方法,以及它所伴隨的非連續性
波函式坍縮。愛因斯坦主張,量子力學是個決定性理論的統計近似。在薛丁格有生的最後一年,寫給玻恩的一封信中,他清楚地表示他不接受
哥本哈根詮釋。
作者簡介
埃爾溫·薛丁格(Erwin Schrodinger,1887—1961年)1887年8月12日出生於
奧地利首都
維也納。1906年至1910年,他就學於維也納大學物理系。1910年獲得博士學位。畢業後,在維也納大學第二物理研究所從事實驗物理的工作。第一次世界大戰期間,他應徵服役於一個偏僻的炮兵要塞,利用閒暇時間研究
理論物理。戰後他仍回到第二物理研究所。1920年他到耶拿大學協助維恩工作。1921年薛丁格受聘到瑞士的蘇黎世大學任數學物理教授,在那裡工作了6年,薛丁格方程就是在這一期間提出的。1927年薛丁格接替普朗克到柏林大學擔任理論物理教授。1933年希特勒上台後,薛丁格對於納粹政權迫害愛因斯坦等傑出科學家的法西斯行為深為憤慨,移居牛津,在馬達倫學院任
訪問教授。同年他與
狄拉克共同獲得諾貝爾物理學獎。
 埃爾溫·薛丁格
埃爾溫·薛丁格 1936年他回到奧地利任格拉茨大學理論物理教授。不到兩年,奧地利被納粹併吞後,他又陷入了逆境。1939年10月流亡到愛爾蘭首府都柏林,就任都柏林高級研究所所長,從事
理論物理研究。在此期間還進行了科學哲學、生物物理研究,頗有建樹。出版了《生命是什麼》一書,試圖用
量子物理闡明
遺傳結構的穩定性。1956年薛丁格回到了奧地利,被聘為維也納大學理論物理教授,奧地利政府給予他極大的榮譽,設定了以薛丁格命名的國家獎金,由奧地利科學院授予。
具體介紹
數學形式
一維薛丁格方程
三維薛丁格方程
定態薛丁格方程
單粒子薛丁格方程的數學表達形式
這是一個二階線性偏微分方程,ψ(x,y,z)是待求函式,它是x,y,z三個變數的複數函式(就是說函式值不一定是實數,也可能是虛數)。式子最左邊的倒三角是拉普拉斯算符,意思是分別對ψ(x,y,z)的梯度求散度。
物理含義
這是一個描述一個粒子在三維勢場中的定態薛丁格方程。所謂勢場,就是粒子在其中會有勢能的場,比如
電場就是一個帶電粒子的勢場;所謂
定態,就是假設波函式不隨時間變化。其中,E是粒子本身的能量;U(x,y,z)是描述勢場的函式,假設不隨時間變化。薛丁格方程有一個很好的性質,就是時間和空間部分是相互分立的,求出
定態波函式的空間部分後再乘上時間部分
以後就成了完整的波函式了。
薛丁格方程的解——波函式的性質
簡單系統,如氫原子中電子的薛丁格方程才能求解,對於複雜系統必須近似求解。因為對於有Z 個電子的
原子,其電子由於禁止效應相互作用勢能會發生改變,所以只能近似求解。近似求解的方法主要有
變分法和
微擾法。
在束縛態邊界條件下並不是E 值對應的所有解在物理上都是可以接受的。
主量子數、
角量子數、
磁量子數都是薛丁格
方程的解。要完整描述電子狀態,必須要四個
量子數。自旋磁量子數不是薛丁格方程的解,而是作為實驗事實接受下來的。
主量子數n和能量有關的量子數。
原子具有分立
能級,能量只能取一系列值,每一個波函式都對應相應的能量。氫原子以及
類氫原子的分立值為:
,n 越大能量越高電子層離核越遠。主量子數決定了電子出現的最大幾率的區域離核遠近,決定了電子的能量。N=1,2,3,……;常用K、L、M、N……表示。
角量子數l和能量有關的量子數。電子在原子中具有確定的
角動量L,它的取值不是任意的,只能取一系列分立值,稱為角動量
量子化。
。l 越大,角動量越大,能量越高,電子云的形狀也不同。l=0,1,2,……常用s,p,d,f,g 表示,簡單的說就是前面說的
電子亞層。角量子數決定了軌道形狀,所以也稱為軌道形狀量子數。s 為球型,p 為啞鈴型,d 為花瓣,f 軌道更為複雜。
磁量子數m是和電子能量無關的量子數。原子中電子繞核運動的軌道角動量,在外磁場方向上的分量是
量子化的,並由量子數m 決定,m 稱為磁量子數。對於任意選定的外磁場方向Z,角動量L 在此方向上的分量L
z只能取一系列分立值,這種現象稱為空間量子化。
。磁量子數決定了原子軌道空間伸展方向,即原子軌道在空間的取向,s 軌道一個方向(球),p 軌道3 個方向,d 軌道5 個,f 軌道7 個……。l 相同,m 不同即形狀相同空間取向不同的原子軌道能量是相同的。不同原子軌道具有相同能量的現象稱為
能量簡併。
能量相同的原子軌道稱為
簡併軌道,其數目稱為簡併度。如p 軌道有3 個簡併軌道,
簡併度為3。簡併軌道在外磁場作用下會產生能量差異,這就是線狀譜在磁場下分裂的原因。
粒子的自旋也產生角動量,其大小取決於自旋磁量子數(m
s)。
電子自旋角動量是
量子化的其值為
,s 為
自旋量子數,自旋角動量的一個分量L
sz 應取下列分立值:
。
原子光譜,在高分辨光譜儀下,每一條光線都是由兩條非常接近的光譜線組成,為解釋這一現象提出了粒子的自旋。電子的自旋表示電子的兩種不同狀態,這兩種狀態有不同的自旋角動量。
電子的自旋不是機械的自身旋轉,它是本身的內稟屬性,也是新的自由度,如質量和電荷一樣是它的內在屬性,電子的自旋角動量:ħ /2。
對應關係
希爾伯特空間與薛丁格方程
一般,物理上將物理狀態與希爾伯特空間上的向量(vector),物理量與希爾伯特空間上的算符相對應。這種形式下的薛丁格方程為
H為哈密頓算符。這個方程在這個形式下充分顯示出了時間與空間的對應性(時間與能量相對應,正如空間與動量相對應,後述)。這種算符(
物理量)不隨時間變化而狀態隨時間變化的對自然現象的描述方法被稱為薛丁格繪景,與之對應的是海森伯繪景。
空間坐標算符x與其對應的動量算符p滿足以下交換關係:
所謂的薛丁格表示就是將空間算符直接作為x,而動量算符為下面的包含微分的微分算符:
 埃爾溫·薛丁格
埃爾溫·薛丁格



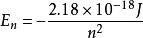




 埃爾溫·薛丁格
埃爾溫·薛丁格