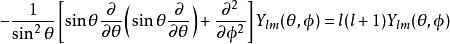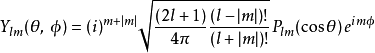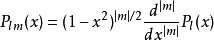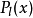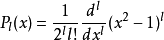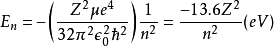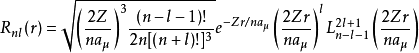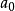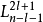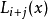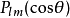類氫原子(hydrogen-like atom)是只擁有一個
電子的
原子,與氫原子同為等電子體,例如,He
+, Li
2+, Be
3+與B
4+等等都是類氫原子,又稱為“類氫離子”。類氫原子只含有一個
原子核與一個電子,是個簡單的二體系統,系統內的作用力只跟二體之間的距離有關,是反平方連心力。這反平方連心力二體系統不需再加理想化,簡單化。描述這系統的(非相對論性的)
薛丁格方程式有
解析解,也就是說,解答能以有限數量的常見函式來表達。滿足這薛丁格方程式的波函式可以完全地描述電子的量子行為。在
量子力學里,類氫原子問題是一個很簡單,很實用,而又有解析解的問題。所推演出來的基本物理理論,又可以用簡單的實驗來核對。所以,類氫原子問題是個很重要的問題。
稱滿足上述系統的薛丁格方程式的波函式為單電子波函式,或類氫原子波函式。類氫原子波函式是單電子
角動量算符 L 與其 z-軸分量算符 L
z的本徵函式。由於能量本徵值 E
n 跟量子數 l,m 無關,而只跟
主量子數 n 有關。所以,類氫原子波函式可以由主量子數 n 、
角量子數 l 、
磁量子數 m獨特地決定。因為
構造原理,還必須加上
自旋量子數 m
s = ± 1 / 2。對於多電子原子,這原理限制了電子構型的四個量子數。對於類氫原子,所有簡併的軌域形成了一個電子層;每一個電子層都有其獨特的主量子數 n.這主量子數決定了電子層的能量。
除了氫原子(電中性)以外,類氫原子都是離子,都帶有正電荷量 e ( Z − 1 );其中,e, Z 是原子序數。
薛丁格方程
類氫原子問題的薛丁格方程式為
其中,ϵ
0是
真空電容率,Z是原子序數,e 是單位電荷量,r是電子離原子核的距離。
猜想這薛丁格方程式的波函式解 ψ(r,θ,ϕ)是徑向函式 R
nl(r) 與
球諧函式 Y
lm(θ,ϕ)的乘積:
角向部分
參數為天頂角和方位角的球諧函式,滿足角部分方程式
其中,非負整數 l是軌角動量的角量子數。磁量子數 m(滿足 −l≤m≤l )是軌角動量對於 z-軸的(量子化的)投影。不同的 l與 m給予不同的軌角動量函式解答 Ylm:
徑向部分解答
徑向函式滿足一個一維薛丁格方程式:
方程式左邊的第二項可以視為離心力位勢,其效應是將徑向距離拉遠一點。
除了量子數 ℓ 與 m以外,還有一個
主量子數 n。為了滿足 R
nl(r) 的邊界條件,n必須是正值整數,能量也離散為
能級 。隨著量子數的不同,函式 R
nl(r)與 Y
lm都會有對應的改變。按照慣例,規定用波函式的下標符號來表示這些量子數。這樣,徑向函式可以表達為
其中,
。
近似於波耳半徑
。假若,原子核的質量是無限大的,則
,並且,約化質量等於電子的質量,
。
是廣義拉格耳多項式,定義為
其中l<n 。
自旋-軌道作用
電子的總角動量必須包括電子的
自旋。在一個真實的原子裡,因為電子環繞著原子核移動,會感受到磁場。電子的
自旋與
磁場產生作用 ,這現象稱為
自旋-軌道作用。當將這現象納入計算,自旋與角動量不再是保守的,可以將此想像為電子的
進動。為了維持
保守性,必須取代量子數 l、m與自旋的投影 m
s,而以量子數 j,m
j 來計算總角動量。
精細結構
非相對論性,無
自旋的電子產生的譜線稱為粗略結構。類氫原子的粗略結構只跟主量子數 n有關。可是,更精確的模型,考慮到相對論效應與自旋-軌道效應,能夠分解能級的
簡併,使譜線能更精細地分裂。相對於粗略結構,精細結構是一個 (Zα)
2效應;其中,Z是
原子序數,α是
精細結構常數。