勒讓德多項式是描述矩形表面和口徑的另外一組多項式集合,它的優點是具有正交性。由於存在正交性條件,高階項係數趨於零,並且增加和刪除一個項對其他項沒有影響。不過,這個多項式集合通常不在光學設計軟體中使用。
基本介紹
- 中文名:勒讓德多項式
- 外文名:Legendre Polynomials
- 所屬領域:數理科學
- 創造人:勒讓德
- 優點:具有正交性
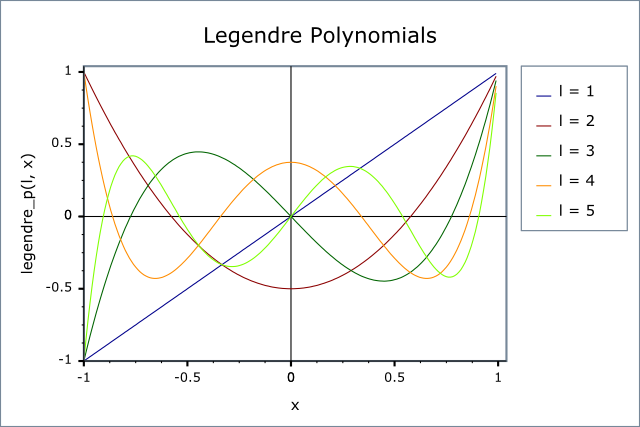
勒讓德多項式是描述矩形表面和口徑的另外一組多項式集合,它的優點是具有正交性。由於存在正交性條件,高階項係數趨於零,並且增加和刪除一個項對其他項沒有影響。不過,這個多項式集合通常不在光學設計軟體中使用。
勒讓德多項式是描述矩形表面和口徑的另外一組多項式集合,它的優點是具有正交性。由於存在正交性條件,高階項係數趨於零,並且增加和刪除一個項對其他項沒有影響。...
在數學中,勒讓德函式Pλ,Qλ和相關的勒讓德函式Pλμ,Qλμ是勒讓德多項式與非整數度的泛化。...
勒讓德方程的解可寫成標準的冪級數形式。當方程滿足 |x| < 1 時,可得到有界解(即解級數收斂)。並且當n 為非負整數,即n = 0, 1, 2,... 時,在x =...
連帶勒讓德函式有兩類:第一類連帶勒讓德函式、第二類連帶勒讓德函式。連帶勒讓德函式是連帶勒讓德方程的解。...
'''大q-勒讓德多項式'''是一個以[[基本超幾何函式]]定義的正交多項式Roelofp443: : ==正交性== ...
當α=1/2時,方程式減少到勒讓德方程,蓋根堡多項式減少到勒讓德多項式。當α=0時,方程式減少到切比雪夫微分方程,蓋根堡多項式減少到第一類的切比雪夫多項式。...
雅可比多項式是在區間【-1,1】上關於權函式組成正交系的多項式,又稱超幾何多項式。雅可比多項式在一些條件下可化為勒讓德多項式或切比雪夫多項式。...
法國數學家、天文學家勒讓德(Legendre, Asrien-Marie,1752-1833)出生在一個比較富有的家庭,從小受到良好的教育。18歲時,通過了數學物理的畢業論文答辯。...
在關於行星形狀和球體引力的研究中,勒讓德引進了著名的“勒讓德多項式”,發現了它的許多性質。他還研究了Β函式和Γ函式(他把這兩個函式分別稱為第一類和第二類...
高斯一勒讓德求積公式(Gauss-Legendre qua-drature)是一種高斯型求積公式,用來解決函式問題。...
阿德利昂·瑪利·埃·勒讓德(公元1752年9月18日- 1833年1月10日)為法國數學家,生於巴黎,卒於同地。約1770年畢業於馬扎蘭學院。1775年任巴黎軍事學院數學教授...
正交多項式是由多項式構成的正交函式系的通稱。正交多項式最簡單的例子是勒讓德多項式,此外還有雅可比多項式、切比雪夫多項式、拉蓋爾多項式、埃爾米特多項式等,它們在...
它是病態矩陣,因此,這種算法只適合於n≤3的情形,為此,求最小平方逼近多項式可利用勒讓德多項式 ,設 ,則在[-1,1]上的最小平方逼近多項式為 ,其中 。...
7.1正交多項式7.1.1正交函式族7.1.2正交多項式的性質7.1.3勒讓德多項式7.1.4切比雪夫多項式7.1.5切比雪夫多項式零點插值7.2最佳平方逼近...
本書內容包括特殊函式(伽馬函式、超幾何函式、勒讓德多項式和貝塞爾函式等)和積分變換(傅立葉積分變換、拉普拉斯積分變換和亨格爾積分變換等)。...
這個結論被稱為阿培里定理。最初的證明很長,而且晦澀難懂,幸好不久後發現了更為簡潔的證明,只需要用到勒讓德多項式。現在還不能確定阿培里常數是否是超越數。...
7.3 勒讓德多項式 7.4 廣義冪級數解法 7.5 貝塞爾函式 第八章 定性理論與分支理論初步 8.1 動力系統,相空間與軌線 8.2 解的穩定性 8.2.1 李雅普諾夫穩...
勒讓德函式是有3個正則奇點的二階線性常微分方程的解,可以用以不同的形式用超幾何函式表示,例如很多多項式,例如賈可比多項式P(α,β) n及其特殊情形勒讓德...
全書共分九章,前四章及第七、第八章介紹數學物理方程的基本概念和常用解法;第五、六兩章分別討論了貝塞爾函式與勒讓德多項式的基本性質及在求解數學物理方程定解...
全書共分九章,前四章及第七、第八章介紹數學物理方程的基本概念和常用解法;第五、六兩章分別討論了貝塞爾函式與勒讓德多項式的基本性質及在求解數學物理方程定解...
其中j} (kr)是L階球貝塞爾函式,P}<cos B)是L次勒讓德多項式.若將r和B理解為球坐標,則e}k}}ose=少‘表示沿z方向傳播的平面波(等相位面為z一常數)相位...
全書共分九章,前四章及第七、第八章介紹數學物理方程的基本概念和常用解法;第五、六兩章分別討論了貝塞爾函式與勒讓德多項式的基本性質及在求解數學物理方程定解...
