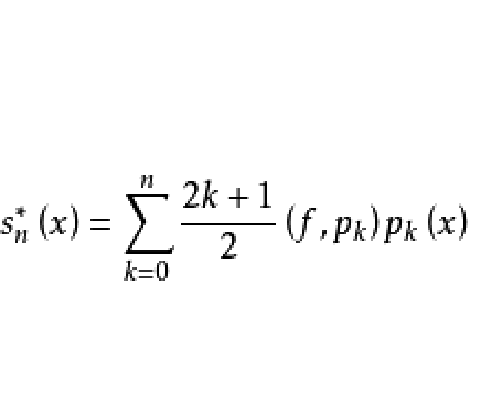最小平方逼近多項式(polynomials of least square approximation)是一種逼近多項式,指最佳均方逼近中,取逼近函式類為多項式集合Hn時的多項式。
基本介紹
- 中文名:最小平方逼近多項式
- 外文名:polynomials of least square approximation
- 所屬學科:數學
- 所屬問題:計算數學(數值逼近)
基本介紹,曲線擬合的最小二乘法,問題描述,最小二乘法表述,最小平方逼近多項式的存在性,
基本介紹
當 時,設逼近多項式
時,設逼近多項式 ,記
,記






曲線擬合的最小二乘法
問題描述
在生產實踐和科學研究中,時常需要從一組測定的數據去求函式 的近似表達式。從圖形上看,這個問題就是根據曲線
的近似表達式。從圖形上看,這個問題就是根據曲線 上已給的(n+1)個點
上已給的(n+1)個點 ,求作該曲線的近似圖形。插值問題就屬於這種問題。
,求作該曲線的近似圖形。插值問題就屬於這種問題。



不過插值問題要求近似曲線 嚴格地通過所給的(n+1)個點
嚴格地通過所給的(n+1)個點 ,這一要求將會使近似曲線
,這一要求將會使近似曲線 保留數據的全部測試誤差(通過實驗所得到的數據總是帶有測試誤差),如果個別數據的精度很差(誤差很大),那么插值的效果顯然是不理想的。另外,一般來說,這樣的插值多項式必須是n次的,n較大時,插值多項式次數也比較高,這對於函式性質分析和實際計算都是不方便的。
保留數據的全部測試誤差(通過實驗所得到的數據總是帶有測試誤差),如果個別數據的精度很差(誤差很大),那么插值的效果顯然是不理想的。另外,一般來說,這樣的插值多項式必須是n次的,n較大時,插值多項式次數也比較高,這對於函式性質分析和實際計算都是不方便的。



為了降低多項式次數,又在給定數據的基礎上反映數據的一般趨勢,放棄必須通過所有(n+1)個點的要求,但希望這條多項式曲線儘量接近每一點,也就是:尋求一個次數低於n的m次多項式,使它在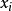 點上取值儘量接近
點上取值儘量接近 ,這就是代數曲線擬合問題。
,這就是代數曲線擬合問題。

最小二乘法表述
設所求的多項式為



由於曲線 不一定通過所有點
不一定通過所有點 ,所以諸
,所以諸 不會全為零。
不會全為零。



所謂最小二乘法,就是選擇 ,使
,使








最小平方逼近多項式的存在性
由微分學知,若使 達到最小值,則
達到最小值,則 必滿足:
必滿足:






定理1式(1)的解是存在唯一的。
定理2式(1)的解 使
使 達到最小值。
達到最小值。