實際工作中，變數間未必都有線性關係，如服藥後血藥濃度與時間的關係；疾病療效與療程長短的關係；毒物劑量與致死率的關係等常呈曲線關係。曲線擬合（curve fitting）是指選擇適當的曲線類型來擬合觀測數據，並用擬合的曲線方程分析兩變數間的關係。
基本介紹
- 中文名：曲線擬合
- 外文名：curve-fitting
- 曲線擬合：一種數據處理方法
- 定義：用解析表達式逼近離散數據的方法
- 常用函式：指數函式、對數函式等
- 曲線直線化：是曲線擬合的重要手段之一
簡介,意義,常用函式,指數函式,對數函式,冪函式,步驟,
簡介
用連續曲線近似地刻畫或比擬平面上離散點組所表示的坐標之間的函式關係的一種數據處理方法。用解析表達式逼近離散數據的一種方法。在科學實驗或社會活動中，通過實驗或觀測得到量x與y的一組數據對(xi，yi)（i=1，2，…m），其中各xi是彼此不同的 。人們希望用一類與數據的背景材料規律相適應的解析表達式，y=f(x，c）來反映量x與y之間的依賴關係，即在一定意義下“最佳”地逼近或擬合已知數據。f(x，c)常稱作擬合模型 ，式中c=(c1，c2，…cn)是一些待定參數。當c在f中線性出現時，稱為線性模型，否則稱為非線性模型。有許多衡量擬合優度的標準，最常用的一種做法是選擇參數c使得擬合模型與實際觀測值在各點的殘差(或離差)ek=yk－f(xk，c)的加權平方和達到最小，此時所求曲線稱作在加權最小二乘意義下對數據的擬合曲線。有許多求解擬合曲線的成功方法，對於線性模型一般通過建立和求解方程組來確定參數，從而求得擬合曲線。至於非線性模型，則要藉助求解非線性方程組或用最最佳化方法求得所需參數才能得到擬合曲線，有時稱之為非線性最小二乘擬合。
曲線擬合
曲線擬合公式推導
曲線擬合曲線擬合公式推導曲線擬合：貝塞爾曲線與路徑轉化時的誤差。值越大，誤差越大；值越小，越精確。
意義
曲線直線化是曲線擬合的重要手段之一。對於某些非線性的資料可以通過簡單的變數變換使之直線化，這樣就可以按最小二乘法原理求出變換後變數的直線方程，在實際工作中常利用此直線方程繪製資料的標準工作曲線，同時根據需要可將此直線方程還原為曲線方程，實現對資料的曲線擬合。
常用函式
指數函式
指數函式(exponential function)的標準式形式為
對上式兩邊取自然對數，得
更一般的指數函式
式中k為一常量，往往未知, 套用時可試用不同的值。
對數函式
對數函式（lograrithmic function）的標準式形式為
利用換底公式可得
一般形式為
a>1時，Y隨X增大而增大，先快後慢；0<a<1時，Y隨X增大而減少，先快後慢。當以Y和lnX繪製的散點圖呈直線趨勢時，可考慮採用對數函式描述Y與X之間的非線性關係，式中的b和a分別為斜率和截距。
冪函式
冪函式（power function）的標準式形式為
式中b>0時，Y隨X增大而增大；b<0時，Y隨X增大而減少。
對上式兩邊取對數，得
所以，當以lnY和lnX繪製的散點圖呈直線趨勢時，可考慮採用冪函式來描述Y和X間的非線性關係，lna和b分別是截距和斜率。
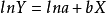
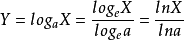
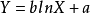
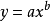
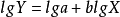
曲線擬合