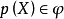最小二乘法:歷史,適用領域,線性最小二乘的基本公式,原理,方法,公式,擬合,課題,

最小二乘法（又稱最小平方法）是一種數學最佳化技術。它通過最小化誤差的平方和尋找數據的最佳函式匹配。利用最小二乘法可以簡便地求得未知的數據，並使得這些求得的數據與實際數據之間誤差的平方和為最小。最小二乘法還可用於曲線擬合。其他一些最佳化問題也可通過最小化能量或最大化熵用最小二乘法來表達。

基本介紹

中文名：最小二乘法
外文名：Least squares
別稱：最小平方法
提出者：馬里·勒讓德
提出時間：1806年
套用學科：數學
適用領域範圍：代數
適用領域範圍：曲線擬合

歷史,適用領域,線性最小二乘的基本公式,原理,方法,公式,擬合,課題,思考與練習,實例,

歷史

1801年，義大利天文學家朱賽普·皮亞齊發現了第一顆小行星穀神星。經過40天的跟蹤觀測後，由於穀神星運行至太陽背後，使得皮亞齊失去了穀神星的位置。隨後全世界的科學家利用皮亞齊的觀測數據開始尋找穀神星，但是根據大多數人計算的結果來尋找穀神星都沒有結果。時年24歲的高斯也計算了穀神星的軌道。奧地利天文學家海因里希·奧爾伯斯根據高斯計算出來的軌道重新發現了穀神星。

高斯使用的最小二乘法的方法發表於1809年他的著作《天體運動論》中。

法國科學家勒讓德於1806年獨立發明“最小二乘法”，但因不為世人所知而默默無聞。

勒讓德曾與高斯為誰最早創立最小二乘法原理髮生爭執。

1829年，高斯提供了最小二乘法的最佳化效果強於其他方法的證明，因此被稱為高斯-馬爾可夫定理。（來自於wikipedia）

適用領域

代數，數學學科

線性最小二乘的基本公式

考慮超定方程組（超定指未知數小於方程個數）：

其中m代表有m個等式，n代表有 n 個未知數

，m>n ；將其進行向量化後為：

，

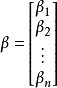
顯然該方程組一般而言沒有解，所以為了選取最合適的

讓該等式"儘量成立"，引入殘差平方和函式S

（在統計學中，殘差平方和函式可以看成n倍的均方誤差MSE）

當

時，

取最小值，記作：

通過對

進行微分求最值，可以得到：

如果矩陣

非奇異則

有唯一解：

原理

在我們研究兩個變數（x,y）之間的相互關係時，通常可以得到一系列成對的數據（x1,y1.x2,y2... xm,ym）；將這些數據描繪在x -y直角坐標系中，若發現這些點在一條直線附近，可以令這條直線方程如（式1-1）。

（式1-1）

其中：a0、a1 是任意實數

為建立這直線方程就要確定a0和a1，套用《最小二乘法原理》，將實測值Yi與利用計算值Yj（Yj=a0+a1Xi）（式1-1）的離差（Yi-Yj）的平方和

最小為“最佳化判據”。

令：φ =

（式1-2)

把（式1-1）代入（式1-2）中得：

φ =

（式1-3)

當

最小時，可用函式 φ 對a0、a1求偏導數，令這兩個偏導數等於零。

∑2(a0 + a1*Xi - Yi）=0（式1-4)

∑2Xi（a0 +a1*Xi - Yi）=0（式1-5)

亦即：

na0 + （∑Xi ) a1 = ∑Yi （式1-6)

（∑Xi ) a0 + （∑Xi^2 ) a1 = ∑（Xi*Yi) （式1-7)

得到的兩個關於a0、 a1為未知數的兩個方程組，解這兩個方程組得出：

a0 = （∑Yi) / n - a1（∑Xi) / n （式1-8)

a1 = [n∑(Xi Yi) - （∑Xi ∑Yi)] / (n∑Xi^2 -∑Xi∑Xi)（式1-9)

這時把a0、a1代入（式1-1）中，此時的(式1-1）就是我們回歸的一元線性方程即：數學模型。

在回歸過程中，回歸的關聯式不可能全部通過每個回歸數據點（x1,y1. x2,y2...xm,ym），為了判斷關聯式的好壞，可藉助相關係數“R”，統計量“F”，剩餘標準偏差“S”進行判斷；“R”越趨近於 1 越好；“F”的絕對值越大越好；“S”越趨近於 0 越好。

R = [∑XiYi - m （∑Xi / m）（∑Yi / m)]/ SQR{[∑Xi2 - m （∑Xi / m)2][∑Yi2 - m （∑Yi / m)2]} （式1-10) *

在（式1-10）中，m為樣本容量，即實驗次數；Xi、Yi分別為任意一組實驗數據X、Y的數值。

方法

以最簡單的一元線性模型來解釋最小二乘法。什麼是一元線性模型呢？監督學習中，如果預測的變數是離散的，我們稱其為分類（如決策樹，支持向量機等），如果預測的變數是連續的，我們稱其為回歸。回歸分析中，如果只包括一個自變數和一個因變數，且二者的關係可用一條直線近似表示，這種回歸分析稱為一元線性回歸分析。如果回歸分析中包括兩個或兩個以上的自變數，且因變數和自變數之間是線性關係，則稱為多元線性回歸分析。對於二維空間線性是一條直線；對於三維空間線性是一個平面，對於多維空間線性是一個超平面。

對於一元線性回歸模型, 假設從總體中獲取了n組觀察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。對於平面中的這n個點，可以使用無數條曲線來擬合。要求樣本回歸函式儘可能好地擬合這組值。綜合起來看，這條直線處於樣本數據的中心位置最合理。選擇最佳擬合曲線的標準可以確定為：使總的擬合誤差（即總殘差）達到最小。有以下三個標準可以選擇：

（1）用“殘差和最小”確定直線位置是一個途徑。但很快發現計算“殘差和”存在相互抵消的問題。

（2）用“殘差絕對值和最小”確定直線位置也是一個途徑。但絕對值的計算比較麻煩。

（3）最小二乘法的原則是以“殘差平方和最小”確定直線位置。用最小二乘法除了計算比較方便外，得到的估計量還具有優良特性。這種方法對異常值非常敏感。

最常用的是普通最小二乘法（ Ordinary Least Square，OLS）：所選擇的回歸模型應該使所有觀察值的殘差平方和達到最小。（Q為殘差平方和）- 即採用平方損失函式。

樣本回歸模型：

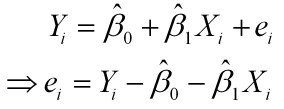
其中e_i為樣本（X_i,Y_i）的誤差。

平方損失函式：

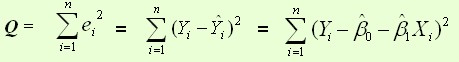
則通過Q最小確定這條直線，即確定β0和β1，把它們看作是Q的函式，就變成了一個求極值的問題，可以通過求導數得到。求Q對兩個待估參數的偏導數：

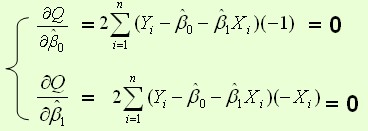
根據數學知識我們知道，函式的極值點為偏導為0的點。

解得：

這就是最小二乘法的解法，就是求得平方損失函式的極值點。

公式

擬合

對給定數據點集合

，在取定的函式類

中，求

，使誤差的平方和

最小，

。從幾何意義上講，就是尋求與給定點集

的距離平方和為最小的曲線y=p(x)。函式p(x)稱為擬合函式或最小二乘解，求擬合函式p(x)的方法稱為曲線擬合的最小二乘法。

最小二乘法的矩陣形式

最小二乘法的矩陣形式為：

其中

為

的矩陣，

為

的列向量，

為

的列向量。如果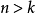

（方程的個數大於未知量的個數），這個方程系統稱為矛盾方程組（Over Determined System），如果

（方程的個數小於未知量的個數），這個系統就是Under Determined System。

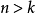
正常來看，這個方程是沒有解的，但在數值計算領域，我們通常是計算

，解出其中的

。比較直觀的做法是求解

，但通常比較低效。其中一種常見的解法是對

進行QR分解（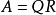

），其中

是

正交矩陣（Orthonormal Matrix），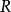

是

上三角矩陣（Upper Triangular Matrix），則有

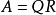
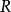
用MATLAB命令

x=R\(Q\b)

可解得

。

最小二乘法的Matlab實現

① 一次函式線性擬合使用polyfit（x,y,1）

②多項式函式線性擬合使用 polyfit（x,y,n），n為次數

擬合曲線

x=[0.5,1.0,1.5,2.0,2.5,3.0]，

y=[1.75,2.45,3.81,4.80,7.00,8.60]。

解：MATLAB程式如下：

x=[0.5,1.0,1.5,2.0,2.5,3.0];y=[1.75,2.45,3.81,4.80,7.00,8.60];p=polyfit(x,y,2)x1=0.5:0.5:3.0;y1=polyval(p,x1);plot(x,y,'*r',x1,y1,'-b')

計算結果為：

p =0.5614 0.8287 1.1560

即所得多項式為y=0.5614x^2+0.8287x+1.15560

③非線性函式使用

lsqcurvefit(fun,x0,x,y)a=nlinfit(x,y,fun,b0)

最小二乘法在交通運輸學中的運用

交通發生預測的目的是建立分區產生的交通量與分區土地利用、社會經濟特徵等變數之間的定量關係，推算規劃年各分區所產生的交通量。因為一次出行有兩個端點，所以我們要分別分析一個區生成的交通和吸引的交通。交通發生預測通常有兩種方法：回歸分析法和聚類分析法。

回歸分析法是根據對因變數與一個或多個自變數的統計分析，建立因變數和自變數的關係，最簡單的情況就是一元回歸分析，一般式為：Y=α+βX式中Y是因變數，X是自變數，α和β是回歸係數。若用上述公式預測小區的交通生成，則以下標 i 標記所有變數；如果用它研究分區交通吸引，則以下標 j 標記所有變數。而運用公式的過程中需要利用最小二乘法來求解，上述公式中的回歸係數根據最小二乘法可得：

其中，式中的X拔是規劃年的自變數值，Y拔是規劃年分區交通生成（或吸引）預測值。

課題

從前面的學習中, 我們知道最小二乘法可以用來處理一組數據, 可以從一組測定的數據中尋求變數之間的依賴關係, 這種函式關係稱為經驗公式. 本課題將介紹最小二乘法的精確定義及如何尋求點與點之間近似成線性關係時的經驗公式. 假定實驗測得變數之間的 n個數據, 則在平面上, 可以得到 n個點 , 這種圖形稱為“散點圖”, 從圖中可以粗略看出這些點大致散落在某直線近旁, 我們認為與之間近似為一線性函式, 下面介紹求解步驟.

考慮函式 y=a+bx, 其中a 和 b是待定常數. 如果離散點完全的在一直線上,可以認為變數之間的關係為一元函式 . 但一般說來, 這些點不可能在同一直線上. 但是它只能用直線來描述時, 計算值與實際值會產生偏差. 當然要求偏差越小越好, 但由於偏差可正可負, 因此不能認為總偏差時, 擬合函式很好地反映了變數之間的關係,但是因為此時每個偏差的絕對值可能很大. 為了改進這一缺陷, 就考慮用平均值來代替 . 但是由於絕對值不易作解析運算, 因此, 進一步用殘差平方和函式來度量總偏差. 偏差的平方和最小可以保證每個偏差都不會很大. 於是問題歸結為確定擬合函式中的常數和使殘差平方和函式最小. 通過這種方法確定係數的方法稱為最小二乘法.

由極值原理得 , 即

解此聯立方程得

(*)

問題 I 為研究某一化學反應過程中, 溫度 ℃)對產品得率 (%)的影響, 測得數據如下:

溫度 ℃)

100 110 120 130 140 150 160 170 180 190

得率 (%)

45 51 54 61 66 70 74 78 85 89

(1) 利用“ListPlot”函式, 繪出數據的散點圖(採用格式: ListPlot[{ , , …, }, Prolog->AbsolutePointSize[3]] );

(2) 利用“Line”函式, 將散點連線起來, 注意觀察有何特徵? (採用格式: Show[Graphics[Line[{ , , …, }]] , Axes->True ]) ;

(3) 根據公式(*), 利用“Apply”函式及集合的有關運算編寫一個小的程式, 求經驗公式 ;

(程式編寫思路為: 任意給定兩個集合A (此處表示溫度)、B(此處表示得率), 由公式(*)可定義兩個二元函式(集合A和B為其變數)分別表示和 . 集合A元素求和: Apply[Plus,A] 表示將加法施加到集合A上, 即各元素相加, 例如Apply[Plus,{1,2,3}]=6;Length[A]表示集合A 元素的個數, 即為n; A.B表示兩集合元素相乘相加;A*B表示集合A與B元素對應相乘得到的新的集合.)

(4) 在同一張圖中顯示直線及散點圖;

(5) 估計溫度為200時產品得率.

然而, 不少實際問題的觀測數據 , , …, 的散點圖明顯地不能用線性關係來描敘, 但確實散落在某一曲線近旁, 這時可以根據散點圖的輪廓和實際經驗, 選一條曲線來近似表達與的相互關係.

問題 II 下表是美國舊轎車價格的調查資料, 今以表示轎車的使用年數, (美元)表示相應的平均價格, 求與之間的關係.

使用年數

1 2 3 4 5 6 7 8 9 10

平均價格

2651 1943 1494 1087 765 538 484290 226 204

(1) 利用“ListPlot”函式繪出數據的散點圖, 注意觀察有何特徵?

(2) 令 , 繪出數據的散點圖, 注意觀察有何特徵?

(3) 利用“Line”函式, 將散點連線起來, 說明有何特徵?

(4) 利用最小二乘法, 求與之間的關係;