樣本容量是指一個樣本中所包含的單位數,一般用n 表示,它是抽樣推斷中非常重要的概念。樣本容量的大小與推斷估計的準確性有著直接的聯繫,即在總體既定的情況下,樣本容量越大其統計估計量的代表性誤差就越小,反之,樣本容量越小其估計誤差也就越大。
基本介紹
- 中文名:樣本容量
- 外文名:sample size
- 又稱:樣本大小
- 意義:一個樣本中所包含的個案或單元數
- 因素:精確度、同質性、財力
- 套用學科:統計學
簡介
 相關書籍
相關書籍解釋
詳細內容
相關定義
最優選擇
意義
樣本個數
公式和方法
公式
計算方法
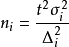




樣本容量是指一個樣本中所包含的單位數,一般用n 表示,它是抽樣推斷中非常重要的概念。樣本容量的大小與推斷估計的準確性有著直接的聯繫,即在總體既定的情況下,樣本容量越大其統計估計量的代表性誤差就越小,反之,樣本容量越小其估計誤差也就越大。
 相關書籍
相關書籍



樣本容量是指一個樣本中所包含的單位數,一般用n 表示,它是抽樣推斷中非常重要的概念。樣本容量的大小與推斷估計的準確性有著直接的聯繫,即在總體既定的情況下,...
樣本量是指總體中抽取的樣本元素的總個數,套用於統計學、數學、物理學等學科。樣本量大小是選擇檢驗統計量的一個要素。由抽樣分布理論可知,在大樣本條件下,如果...
在保證一定的置信區間和置信機率的條件下至少必須抽選的樣本單位數目。根據大數法則,樣本容量和抽樣誤差之間有密切關係。為了避免抽取單位過多或過少,對樣本容量應...
樣本外語(specimen)是觀測或調查的一部分個體,總體是研究對象的全部。總體中抽取的所要考查的元素總稱,樣本中個體的多少叫樣本容量。一般的,樣本的內容是帶著單位...
《社會調查中樣本容量的確定》是2008年5月1日科學出版社出版的圖書,作者是耿修林。本書主要內容包括:樣本容量確定的目標和樣本容量確定的影響因素,樣本統計量的抽樣...
樣本個數是指在一個抽樣方案中所有可能被抽取的樣本的總數量,確切地說,它是可能的樣本個數。其具體數值隨抽樣的方式方法而不同,最常見的算法是根據可重複選排列...
樣本均值(sample mean)又叫樣本均數。即為樣本的均值。均值是表示一組數據集中趨勢的量數,是指在一組數據中所有數據之和再除以這組數據的個數。它是反映數據...
樣本(specimen)是觀測或調查的一部分個體,總體是研究對象的全部。標準差表示的就是樣本數據的離散程度。標準差就是樣本平均數方差的開平方,標準差通常是相對於樣本...
小樣本理論是由英國統計學家威廉.西利.戈塞特(William Sealy Gosset,1876-1937)於20世紀初葉創立的,其中小樣本是指樣本容量小於50(有寫規定為小於等於30)。小樣本...
研究中實際觀測或調查的一部分個體稱為樣本(sample),研究對象的全部稱為總體。為了使樣本能夠正確反映總體情況,對總體要有明確的規定;總體內所有觀察單位必須是同質...
大樣本統計,數理統計學重要分支。研究樣本容量n→∞時,統計量和統計方法的極限性質。在n→∞時得到的性質,叫大樣本性質;根據極限性質而得到的方法,叫大樣本方法。...
樣本總體亦稱“抽樣總體”、“子樣”,簡稱“樣本”。在統計總體中抽取一部分總體單位構成的集合體。在抽樣調查中,樣本又稱作抽樣總體。相應地,原總體又稱作全及...
樣本均值的抽樣分布是所有的樣本均值形成的分布,即μ的機率分布。樣本均值的抽樣分布在形狀上卻是對稱的。隨著樣本量n的增大,不論原來的總體是否服從常態分配,樣本...
小樣本(small sample)是樣本的一種。是指與“大樣本”相對。通常指樣本容量小於或等於30的樣本。必須使用統計量的精確分布來進行統計推斷。...
用做依據的材料,研究中實際觀測或調查的一部分個體稱為樣本(sample),研究對象的全部稱為總體。為了使樣本能夠正確反映總體情況,對總體要有明確的規定;總體內所有...
樣本觀測值中出現狀數最多的數值。樣本眾數反映的是事物的最普遍水平。樣本容量較小時,可以直接求得眾數;當樣本容量較大時,可以根據頻率(數)分布(即變數數列)求...
樣本值是指為了估測總體的特性而對部分個體進行抽取並進行觀測和分析,所抽取個體的觀測數據或者所得到的測量值或測定值就稱為樣本值。...
總體是指考察的對象的全體, 個體是總體中的每一個考察的對象, 樣本是總體中所抽取的一部分個體, 而樣本容量則是指樣本中個體的數目。樣本分布是用來估計總體分布...
小樣本檢驗(small sample test)是統計假設檢驗的一種。與“大樣本檢驗”相對。屬小樣本統計的內容。當檢驗統計量的精確分布已知時,允許隨機樣本的容量”不太大(如...
樣本平均數是統計專業術語,樣本平均數是從一個或多個隨機變數上的數據集合(樣本)計算的統計量。樣本平均值是總體平均值的估計量,其中總體是指採集樣本的集合,是...
子樣本具有多種定義。抽樣調查中,子樣本是進行多階段抽樣所選取的樣本。其形成過程即把抽樣調查的各種方式如簡單隨機抽樣、分層抽樣和整群抽樣相結合,先從總體中...
