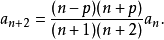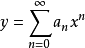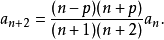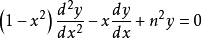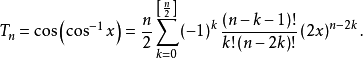第一類切比雪夫多項式

第一類切比雪夫多項式(Chebyshev polynomi-al of the first class)基本的正交多項式之一。

基本介紹

• 中文名：第一類切比雪夫多項式
• 外文名：Chebyshev polynomi-al of the first class
• 適用範圍：數理科學

簡介

第一類切比雪夫多項式是基本的正交多項式之一。

第一類切比雪夫方程（n為非負整數）

的多項式解，

其母函式展開式為

{T_n(x)}在[-1,1]上關於權函式 正交：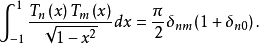

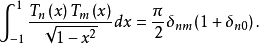
設p_n(x)為在[-1,1]上xⁿ的n-1次最佳逼近多項式，則xⁿ-p_n(x)=2^-n+1T_n(x)。

正交多項式

正交多項式是由多項式構成的正交函式系的通稱。

正交多項式最簡單的例子是勒讓德多項式，此外還有雅可比多項式、切比雪夫多項式、拉蓋爾多項式、埃爾米特多項式等，它們在微分方程、函式逼近等研究中都是極有用的工具。

切比雪夫方程

（Chebysheve quation）

切比雪夫方程是指二階線性常微分方程

其中p為一實常數。該方程是以俄羅斯數學家巴夫尼提·切比雪夫的名字命名的。

方程的解為冪級數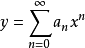 ，其中係數可通過以下遞推關係式計算：