正交多項式是由多項式構成的正交函式系的通稱。
基本介紹
- 中文名:正交多項式
- 外文名:Orthogonal polynomial
- 學科:數學
- 類型:計算機科學
- 用途:統計回歸、最佳平方逼近等
- 概念:由多項式構成的正交函式系的通稱
定義



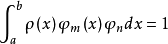
介紹

正交多項式是由多項式構成的正交函式系的通稱。



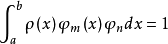

正交多項式是由多項式構成的正交函式系的通稱。...... 對於同一權函式的正交多項式系雖然很多,但是首項係數為 1的正交多項式系或首項係數為正的規範正交多項式系卻...
正交多項式系(system of orthogonal polynomials)是正交函式系的一種。...... 正交多項式系(system of orthogonal polynomials)是正交函式系的一種。中文名 正交多項式...
正交多項式回歸是用正交多項式表安排試驗和回歸分析處理數據。它與用最小二乘法配製的一般多項式回歸不同,其回歸係數的估計是互相獨立的,若統計檢驗某一回歸係數與零...
《多變數的正交多項式》是2003年9月由世界圖書出版公司出版的圖書,作者是C.F.Dunkl,Y.Xu。...
這種情況下,隨n值變化方程的解相應變化,構成一組由正交多項式組成的多項式序列,這組多項式稱為勒讓德多項式(Legendre polynomials)。...
離散變數正交多項式(orthogonal polynomi-als of a discrete variable)自變數只取離散值的正交多項式.設區間[a,司上函式筍(x),必(x)的內積為 其中自變數x為整數...
勒讓德多項式是描述矩形表面和口徑的另外一組多項式集合,它的優點是具有正交性。由於存在正交性條件,高階項係數趨於零,並且增加和刪除一個項對其他項沒有影響。...
澤爾尼克多項式是一個以1953年獲諾貝爾物理學獎荷蘭物理學家弗里茨·澤爾尼克命名的正交多項式,分為奇、偶兩類。...
在數學中,以法國數學家埃德蒙·拉蓋爾(英語:Edmond Laguerre)命名的拉蓋爾多項式定義為拉蓋爾方程的標準解。拉蓋爾多項式,是一列常見的定義於非負實數集上的正交多項式...
在數學中,埃爾米特多項式是一種經典的正交多項式族,得名於法國數學家夏爾·埃爾米特。機率論里的埃奇沃斯級數的表達式中就要用到埃爾米特多項式。在組合數學中,埃爾...
《非傳統區域Fourier變換與正交多項式》是一本由中國科學技術大學出版社在2009年2月1日出版的書籍。...
稱Hn(x)為n階埃爾米特多項式。它在[0,+∞)內有n個零點。常用作插值逼近中的結點。...... 在數學中,埃爾米特多項式是一種經典的正交多項式族,得名於法國數學...
第一類切比雪夫多項式(Chebyshev polynomi-al of the first class)基本的正交多項式之一。...
回歸正交設計,是指試驗方案的結構矩陣具有正交性的回歸設計。是在正交設計基礎上發展起來的,可建立方程,選擇最佳的方案。其突出優點是用很少的處理組合得出完全實施...
正交是線性代數的概念,是垂直這一直觀概念的推廣。作為一個形容詞,只有在一個確定的內積空間中才有意義。若內積空間中兩向量的內積為0,則稱它們是正交的。如果...
通常人們會使用冪級數展開式的形式來描述光學系統的像差。由於澤尼克多項式和光學檢測中觀測到的像差多項式的形式是一致的,因而它常常被用來描述波前特性。但這並不...
在數學中,海曼多項式是一種經典的正交多項式,得名於法國數學家夏爾·海曼。機率論里的埃奇沃斯級數的表達式中就要用到海曼多項式。在組合數學中,海曼多項式是阿佩爾...
Q-拉蓋爾多項式,是一個以基本超幾何函式和Q階乘冪定義的正交多項式。...... Q-拉蓋爾多項式,是一個以基本超幾何函式和Q階乘冪定義的正交多項式。q-LaguerrePolynomia...
《多項式和多項式不等式》是2011-年世界圖書出版公司出版的圖書,作者是加)博爾維恩。...
連續雙哈恩多項式(Continuous dual Hahn polynomials)是一個正交多項式,由廣義超幾何函式定義。...
'''q拉蓋爾多項式'''是一個以[[基本超幾何函式]]和[[Q階乘冪]]定義的正交多項式...... '''是一個以[[基本超幾何函式]]和[[Q階乘冪]]定義的正交多項式 ...
多項式'''是一個以[[基本超幾何函式]]定義的[[正交多項式]]: 關係式*令[[Q拉卡多項式]]中 即得[[雙Q克拉夫楚克多項式]] *令[[雙q哈恩多項式]]中,且...
