基本介紹
- 中文名:拉蓋爾多項式
- 外文名:Laguerre polynomial
- 符號表示:Ln(x)
- 性質:正交表達式
- 命名者:埃德蒙·拉蓋爾
- 套用學科:量子力學,統計學
定義
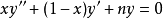
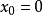
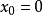
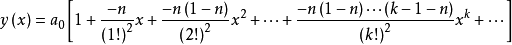
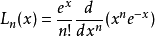
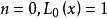
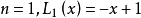
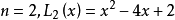
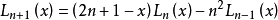
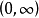
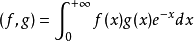
廣義
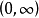
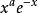
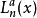
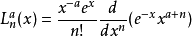

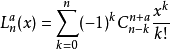

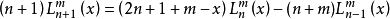
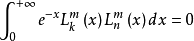
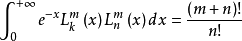
相關恆等式
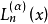
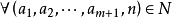
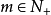
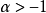
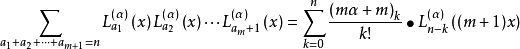

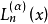
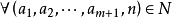
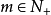
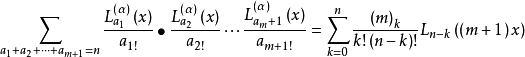
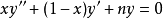
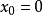
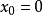
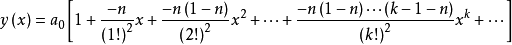
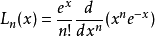
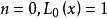
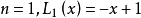
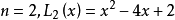
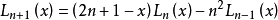
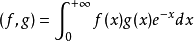
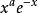
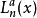
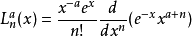

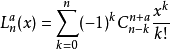

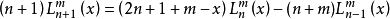
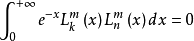
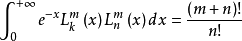
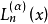
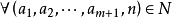
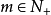
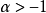
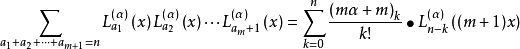

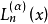
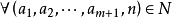
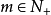
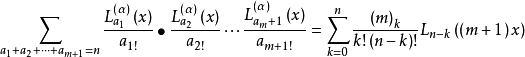
在數學中,以法國數學家埃德蒙·拉蓋爾(英語:Edmond Laguerre)命名的拉蓋爾多項式定義為拉蓋爾方程的標準解。拉蓋爾多項式,是一列常見的定義於非負實數集上的正交多項式...
埃德蒙·尼古拉斯·拉蓋爾(Edmond NicolasLaguerre,1834.4.9-1886.8.14)法國數學家。生於巴勒迪克,卒於同地。畢業於巴黎理工科大學,19歲即發表論文《焦點論》。...
大q-拉蓋爾多項式是一個以基本超幾何函式定義的正交多項式: P_n(x;a,b;q)=\frac{1}{(b^{-1}*q^{-n};q,n)}*_2\Phi_1(q^{-n},aqx^{-1};...
rook多項式,也叫車多項式,是一種生成多項式的方法,用於將非攻擊rook放置在看起來像棋盤的棋盤上;也就是說,沒有兩個車可能在同一行或列中。該板是具有m行和n列...
查理耶多項式(Charlierpolynomials)是一個以瑞典天文學家CarlCharlier命名的正交多項式,由下列拉蓋爾多項式定義 ...
小q拉蓋爾多項式是一個以基本超幾何函式定義的正交多項式 \displaystylep_n(x;a|q)={}_2\phi_1(q^{-n},0;aq;q,qx)=\frac{1}{(a^{-1}q^{-n};...
第一類切比雪夫多項式(Chebyshev polynomi-al of the first class)基本的正交多項式之一。...
Q-拉蓋爾多項式,是一個以基本超幾何函式和Q階乘冪定義的正交多項式。...... Q-拉蓋爾多項式,是一個以基本超幾何函式和Q階乘冪定義的正交多項式。q-LaguerrePolynomia...
第三篇主要討論傅立葉變換和拉普拉斯變換,強調了積分變換的套用;第四篇討論了勒讓德多項式與球函式、貝塞爾函式、厄米多項式和拉蓋爾多項式,特別重視特殊函式的處理...
3.4.2 拉蓋爾方程的冪級數解3.4.3 用計算機軟體計算拉蓋爾多項式3.5 貝塞爾函式3.5.1 貝塞爾方程的冪級數解及貝塞爾函式,3.5.2 諾依曼函式和漢克爾函式3.5.3 用...
為廣義拉蓋爾多項式, 則為角量子數 、磁量子數 所對應的球函式。 同時也得到氫原子能級: 其中基態能量: 通過代入相關量子數,並通過歸一化條件可以得到氫原子基態波...
方程的討論第三篇 特殊函式 第十五章 勒讓德多項式 球函式 第十六章 貝塞爾函式 柱函式 第十七章 埃爾米特多項式和拉蓋爾多項式附錄(Ⅰ)附錄(Ⅱ)習題答案外國人...
17·8 拉蓋爾函式與拉蓋爾多項式17·9 切比雪夫多項式17·10 超幾何函式17·11 合流超幾何函式17·12 橢圓積分與橢圓函式第十八章 數值分析...
3.3.5 正交多項式解集在數值積分中的套用3.4 與多項式的施圖姆-劉維爾系統有關的方程和函式3.4.1 拉蓋爾函式3.4.2 勒讓德函式...
1 定義 2 對稱關係 3 與其他函式的關係 ▪ Meijer G-函式 ▪ 指數函式與誤差函式 ▪ 拉蓋爾函式 4 級數展開 斯塔頓...
