rook多項式,也叫車多項式,是一種生成多項式的方法,用於將非攻擊rook放置在看起來像棋盤的棋盤上;也就是說,沒有兩個車可能在同一行或列中。該板是具有m行和n列的矩形板的正方形的任何子集;我們認為它是允許一個人進入車內的廣場。如果允許所有正方形並且m = n = 8,則棋盤是普通棋盤,如果允許所有正方形並且m = n,則棋盤具有任何尺寸的棋盤。車多項式RB(x)中的xk的係數是k路的數量,其中沒有一個攻擊另一個,可以布置在B的正方形中。車的排列方式使得沒有一對車在同一行或列中。在這個意義上說,一種安排是將車輛定位在一個靜止的不動的板上;如果電路板旋轉或反射,同時保持方塊靜止,則安排不會有所不同。如果行互換或列互換,多項式也保持不變。
基本介紹
- 中文名:rook多項式
- 外文名:Rook polynomial
- 別名:車多項式
定義,完整的板子,匹配多項式,連線矩陣的永久性,
定義
車牌B的車多項式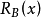 是非攻擊車的排列數的生成函式:
是非攻擊車的排列數的生成函式:
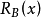
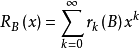
其中 是在板上放置
是在板上放置 個非攻擊車的方法數量。 儘管有記號,但這是一個有限的數字,因為董事會是有限的,所以它可以容納最多數量的非攻擊車。 事實上,不可能有比董事會中行數和列數中的較小者更多的車。
個非攻擊車的方法數量。 儘管有記號,但這是一個有限的數字,因為董事會是有限的,所以它可以容納最多數量的非攻擊車。 事實上,不可能有比董事會中行數和列數中的較小者更多的車。


完整的板子
n×n板上的前幾個多項式是(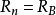 ):
):
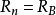

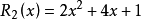


換句話說,這意味著在1×1的電路板上,1路車可以按1路布置,零車也可以按1路布置(空車)。 在一個完整的2×2板上,可以通過2種方式(在對角線上)安排2輛車,可以4種方式安排1輛車,並且可以單向安排0輛車; 等等更大的板子。
對於完整的 矩形板
矩形板 ,我們寫成
,我們寫成 :=
:=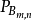 。
。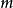 和
和 中較小的一個可以作為
中較小的一個可以作為 的上限,因為如果
的上限,因為如果 ,顯然
,顯然 。 這也在
。 這也在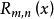 的公式中示出。
的公式中示出。



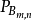
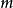




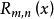
矩形棋盤的rook多項式與廣義拉蓋爾多項式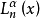 由身份密切相關.
由身份密切相關.
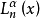

匹配多項式
車多項式是一種匹配多項式的特例,它是圖中k邊匹配次數的生成函式。
車輛多項式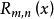 對應於完整的二分圖
對應於完整的二分圖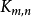 。一般板
。一般板 ,
, 的車多項式對應於具有左頂點
的車多項式對應於具有左頂點 ,
,  ,...,
,...,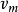 和右頂點
和右頂點 ,
,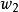 ,...,
,..., 的二分圖和每當方形時的邊
的二分圖和每當方形時的邊 (i允許,即,屬於
(i允許,即,屬於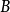 。因此,在某種意義上,車多項式的理論包含在匹配多項式的理論中。
。因此,在某種意義上,車多項式的理論包含在匹配多項式的理論中。
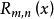
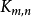




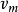

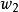


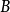
我們推導出一個關於係數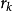 的一個重要事實,我們記得給出了
的一個重要事實,我們記得給出了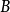 中
中 個非攻擊位置的數量:這些數字是單峰的,即它們增加到最大值然後減小。這遵循Heilmann和Lieb 的定理(通過標準論證)關於匹配多項式的零(與車輛多項式相對應的不同,但在變數變化下相當於它),意味著車輛多項式的所有零都是負實數。
個非攻擊位置的數量:這些數字是單峰的,即它們增加到最大值然後減小。這遵循Heilmann和Lieb 的定理(通過標準論證)關於匹配多項式的零(與車輛多項式相對應的不同,但在變數變化下相當於它),意味著車輛多項式的所有零都是負實數。
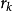
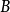

連線矩陣的永久性
對於不完整的方形n×n板,(即不允許在板的方塊的某個任意子集上播放車),計算在板上放置n個車的方法的數量相當於計算0-1矩陣的永久性。
