海曼多項式

在數學中，海曼多項式是一種經典的正交多項式，得名於法國數學家夏爾·海曼。機率論里的埃奇沃斯級數的表達式中就要用到海曼多項式。在組合數學中，海曼多項式是阿佩爾方程的解。物理學中，海曼多項式給出了量子諧振子的本徵態。

基本介紹

• 中文名：海曼多項式
• 外文名：Hermite polynomial
• 又名：埃爾米特多項式
• 時間：1864年
• 提出者：夏爾·海曼
• 領域：數學 物理
• 概念：正交多項式

簡介

海曼多項式是一組正交的多項式。就如許多其他的以人名命名的數學公式一樣，海曼多項式其實也並不是海曼第一個提出的。 拉普拉斯在1810年一篇論文中就給出了埃爾米特多項式的係數，切比雪夫則在 1859 年的一篇論文中詳細的討論了海曼多項式的各種性質。可惜切比雪夫的這篇論文並沒有引起學術圈應由的重視。夏爾·海曼在 1864 年的一篇文章中才提到海曼多項式，這已經比拉普拉斯最初的研究成果晚了54年。

定義

在數學中，海曼多項式是一種經典的正交多項式，得名於法國數學家夏爾·海曼。機率論里的埃奇沃斯級數的表達式中就要用到海曼多項式。在組合數學中，海曼多項式是阿佩爾方程的解。物理學中，海曼多項式給出了量子諧振子的本徵態。

前5個海曼多項式如下：

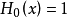
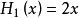
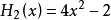
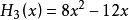
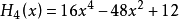
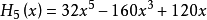
證明

常微分方程：

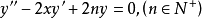
被稱為海曼方程。

x=0 是海曼方程的常點，所以這個微分方程的解可以在 x=0 的鄰域表示為泰勒級數：

對這個級數求導可以得到：

帶入海曼方程得到：

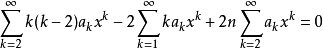
考察 的係數，有 ：

所以：

考察 的係數，有：

所以：

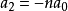
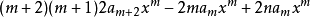
因此可以這樣寫：

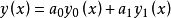
當n是偶數時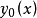， 只有有限項，只要我們將 設為0，那么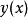 就退化為多項式了。

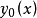
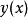
同理，當n是奇數時,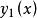 只有有限項，只要我們將 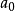設為0,那么 就退化為多項式了。

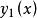
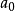
按照這個思路，選擇合適的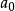 和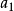 ，便可得到海曼多項式。

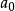
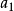
性質

海曼方程可以改寫為斯圖姆-劉維爾型：

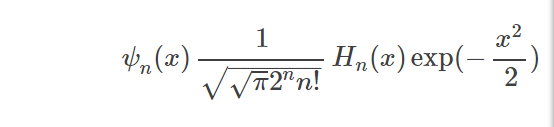
那么顯然有：

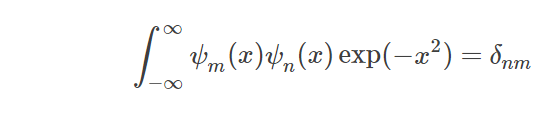
前五個函式如下：

圖像如下：

可以看出埃爾米特函式在 較大時衰減的很快。越往後的海曼函式，非零的區域也越大。第n個海曼函式值過零點的次數是n 次。