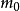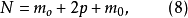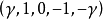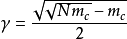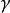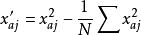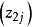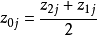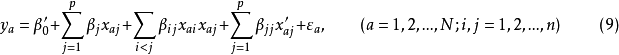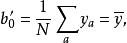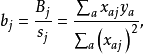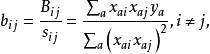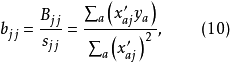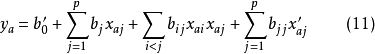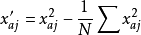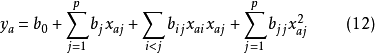基本介紹
回歸正交設計是廣泛套用的回歸設計方法,它主要基於正交試驗的優點(按正交原則安排試驗點稱為正交試驗),利用正交表來安排試驗。如果試驗點是等間距的,那么就可以按正交多項式進行回歸計算,這種計算由於去掉了各因素間的相關性,同時係數矩陣又可以化為對角陣,因此大大簡化了回歸計算的工作量。但是應該指出的是,在安排試驗點時不僅應考慮試驗點的正交性,而且根據這個特點安排試驗應能達到以最合理的試驗點尋求生產工藝的最最佳化區域,然後在這個區域內建立數學模型的目的。這樣把試驗安排與試驗數據的回歸計算統一考慮,就能做到試驗點少但合理、試驗數據分布可靠,計算簡單,回歸方程精度高。按正交多項式回歸模型中自變數的方次來分,回歸設計按類型分為回歸的正交設計、旋轉設計、最優設計、均勻設計以及混料設計等;按次數又分為一次回歸正交設計和二次回歸正交設計。高於二次的正交設計用得較少。
一次回歸正交設計
一次回歸正交設計是指表達試驗結果的回歸方程只有常數項、線性項和線性互動作用項,其
回歸模型為:
多數情況下是利用二水平
正交表安排多因素試驗,各因素水平上限
及下限
確定後取線性變換
對實際水平進行編碼,其中
。
稱為零水平,
稱為變化區間,是編碼值為1的水平間距。經線性變換二水平正交表中的1、2 兩個水平都轉化為編碼值-1及1兩個無量綱的純數。各因素不同水平的取值可能大小不一,轉化為-1及1兩個水平編碼值後即成為多維正立方體因子空間。對回歸模型(1),令
,則模型(1)轉化為
階線性回歸模型。
式(2)中
為p個元素中取2個的組合數,就是兩因素,互動作用的項數、如將兩因素互動作用也理解為1個因素,並將其包括在p個因素之內,則式(2)可簡化表示為
由於式(3)的結構矩陣X如下,它由試驗方案各處理的水平組合所決定。
其中各項因素均經過線性變換為-1及1兩個水平編碼值,除常數項的係數為1外,其餘各列均符合正交條件,所以參數β的最小二乘估計b可簡化為
正交性已消除了結構矩陣中各列之間的相關性,故可剔除不顯著的項。
二次回歸正交設計
二次回歸正交設計是指回歸模型中包括常數項、線性項、線性互動作用項及二次項的回歸正交設計,回歸模型為:
各個因素的水平數必須多於3個才可求出式(7)中的二次項。為了精確繪出二次曲線,常須進行5個水平的試驗,這時處理組合數將多到無法實施,解決這個困難的方法是組合設計。組合設計各實驗單元的處理內容由三部分組成:①
。為二水平正交表中各處理組合。②
。為分布於p個因素坐標軸上距中心點距離為γ的軸點,稱為星號臂。③
。各因素都取零水平的中心點。
二因素及三因素試驗各處理組合在因子空間中的分布如圖1、2。
 圖1 二因素組合設計的因子空間分布
圖1 二因素組合設計的因子空間分布 圖2 三因素組合設計的因子空間分布
圖2 三因素組合設計的因子空間分布組合設計有5個水平
,但處理組合數目比完全實施方案少得多,從而減少過多的剩餘自由度。
為了使式(7)結構矩陣符合正交條件採取了二個措施:①用公式
調整星號臂
取值;②對
列進行中心化變換,得
。當試驗的因素數及各因素水平上限
及下限
確定後,即可用
對試驗水平編碼,與一次回歸正交設計不同的是
。經以上處理後式(7) 成為式(9)
式(9)的結構矩陣內各列符合正交條件,參數
的最小二乘估計b 由式(10) 求得:
對式(11)進行顯著性檢驗後,即可按部分處理有重複的方差分析,再在因子空間中尋優。
回歸正交設計的突出優點是可以用很少的處理組合得出完全實施試驗相同項數的回歸模型,計算過程極為簡單並已消除了
回歸係數之間的相關性,統計性質得到了明顯改善,因此在計算機推薦施肥的多因素肥料試驗中套用甚廣。
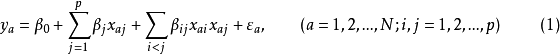
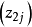
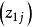
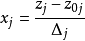
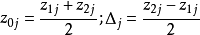
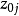
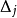
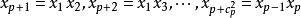
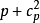
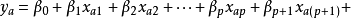
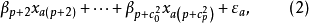
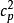
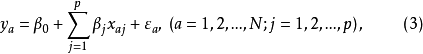
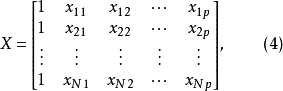
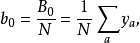

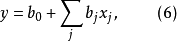
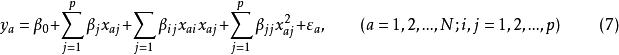
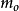
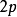
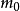
 圖1 二因素組合設計的因子空間分布
圖1 二因素組合設計的因子空間分布 圖2 三因素組合設計的因子空間分布
圖2 三因素組合設計的因子空間分布