非線性系統辨識包括：模型結構確定和參數估計。正交前向回歸（OFR， Orthogonal Forward Regression）算法，是一種有效的確定模型結構的前向回歸算法。該算法能夠從預設模型庫中，依據誤差衰減率（ERR， Error Reduction Ratio）顯著性指標逐項確定有效模型項，成功避免了全局搜尋所帶來的龐大計算。該算法及其改進算法已被廣發套用於非線性系統辨識的各個套用領域。該算法在複雜非線性系統辨識領域有廣闊套用前景，尤其是對系統機理缺乏足夠認識的探索性研究領域。
基本介紹
- 中文名：正交前向回歸算法
- 外文名：Orthogonal Forward Regression Algorithms
非線性系統辨識的特點：
對於線性系統辨識，模型結構確定通常僅需要確定非常有限的幾個結構參數：比如，模型階次。然而對於非線性系統辨識來講，模型結構的確定可能非常複雜。這是因為，非線性的類型非常豐富，除了常見的滯後，飽和，死區，乾摩擦等，還包含大量的非線性函式形式，比如：多項式，指數，周期函式，等等。因此在模型結構未知的情況下精確確定系統中存在的非線性形式至關重要也異常困難。
第二，非線性系統的持續激勵很難滿足。線性系統由於其在狀態空間中的簡單的線性結構，比如，直線，平面或超平面，通常只有唯一的平衡點。而非線性系統在狀態空間的行為要複雜的多，可能包含多個平衡狀態，且可以有不同的吸引子，如：極限環，混沌吸引子等。不同的吸引域將整個狀態空間分割成不同的區域。在每個區域系統行為可能有顯著不同。通過最有輸入設計實現完全激勵系統的所有行為變得非常困難。因此充分激勵一個非線性系統通常不止需要輸入信號要有足夠寬的頻域成分，還要求激勵信號要有豐富的幅值變化，以充分激勵非線性特性及驅動系統遍歷不同的吸引域。
最後，由於複雜的非線性狀態空間結構，使得信息在數據中的分布是不均勻的。不同的數據可能僅包含系統的一些局部行為。系統的某些行為可能大量的存在，而某些特定行為僅存在於少量的觀察數據中。在系統辨識中，這些行為通常會被大量的常見行為所淹沒。
因此非線性系統辨識尤其是模型結構的確定是極大的挑戰，且對算法具有很高的要求。
算法基本原理：
常用的非線性系統辨識方法包括：1. 通過最佳化算法直接確定非線性參數和結構，如符號回歸算法（symbolic regression）；2. 用線性化模型描述系統的局部行為；3. 將非線性問題轉化到線性特徵空間解決，即用非線性特徵（features/terms）的線性組合來描述非線性行為。其中OFR用於解決第三種非線性系統辨識問題。
- 構造足夠大的特徵庫
- 從特徵庫中選取一組解釋能力最強的組合構成一個具有最簡結構形式的模型。然而在此過程中模型結構確定和參數估計是兩個相互耦合的過程，即，參數估計依賴於模型結構，而考核一個模型結構的優劣又依賴於模型係數。因此模型結構的確定通常是一個冗雜的疊代試湊過程。其核心原因在於在同一模型中項與項之間相互不正交，我們無法單獨的衡量模型庫中每一個項的單獨貢獻度。OFR通過在回歸過程中對當前考慮的項逐一正交化處理從而實現模型結構確定和參數估計得解耦。
- 正交化過程可以通過格萊姆-施密特方法實
- ERR（Error Reduction Ratio）指標
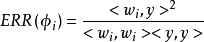
其中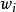
是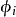
的正交化形式
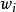
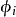
OFR算法可以總結為如下步驟：
- 第一步，計算模型庫中所有項的ERR值，並選擇對應ERR最大的項作為模型的第一項；
- 第 k 步，將模型庫中剩餘的模型項與前 k-1 項逐一正交，並計算對應的ERR值，選擇ERR值最大的項作為第 k 項；
- 重複步驟 2 直至模型有足夠強的描述能力；
- 模型校驗。
算法優點：
- OFR 是一種快速算法。當模型結構未知的情況下，備選模型庫一般非常大。在這種情況下基於比較所有可能模型組合的全局搜素算法通常因為龐大的計算量而無法實施。比如，從>1000個解釋變數中選擇有效的模型項組成一個簡單模型結構。
- OFR 可以基於數據給出一個簡單的模型結構。
- 對絕大多數工程及科學系統，OFR 給出的模型結構是最優模型結構。
改進算法：
疊代正交前向回歸（iOFR， ierative Orthogonal Forward Regression）
超正交前行回歸（UOFR， Ultra Orthogonal Forward Regression）
