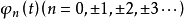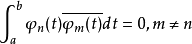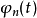正交多項式系（system of orthogonal polynomials）是正交函式系的一種。
基本介紹
- 中文名：正交多項式系
- 外文名：system of orthogonal polynomials
- 適用範圍：數理科學
簡介,常見正交多項式系,正交函式系,
簡介
正交多項式系是正交函式系的一種。
設在區間(a,b)上給定權函式ρ(x)（ρ≥0，且幾乎處處有ρ(x)>0），並定義(a,b)上函式f(x),g(x)的內積為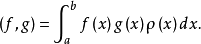
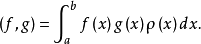
將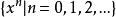
按施密特方法關於ρ(x)正交化，適當規定最高次項的係數，即可得到在(a,b)上關於ρ(x)的正交多項式{p n(x)}。它們在函式空間
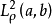內是完備的。 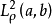為滿足(f,f)<+∞的函式f(x)所構成的空間。
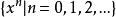
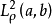
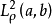
常見正交多項式系
常見的正交多項式系如下表：
pn(x) | a | b | 權函式ρ(x) | 特殊值 |
雅可比多項式  | -1 | 1 |  |  |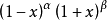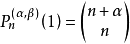
格根鮑爾多項式 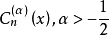 | -1 | 1 |  |  |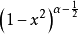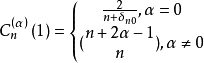
第一類切比雪夫多項式 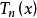 | -1 | 1 | |  |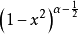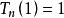
第二類切比雪夫多項式 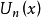 | -1 | 1 | |  |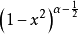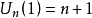
勒讓德多項式 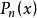 | -1 | 1 | 1 |  |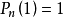
廣義拉蓋爾多項式 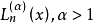 | 0 | +∞ |  |  |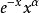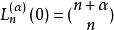
拉蓋爾多項式 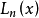 | 0 | +∞ |  |  |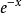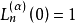
埃爾米特多項式  | -∞ | +∞ |  |  |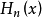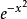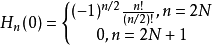
正交函式系
(orthogonal system of functions)
正交函式系是一類特殊的函式系。
對於給定區間[a,b]上的函式系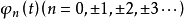
，如果滿足
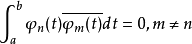則稱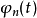
是[a,b]上的正交函式系。
