基本介紹
- 中文名:定態
- 外文名:stationary state
- 含義:微觀粒子所處的一種狀態類型
- 特點:具有確定的能量
- 範疇:量子力學
- 函式表示:Ψ(x,y,z)exp(-i2πEt/h)
概述
 定態示意圖
定態示意圖詳述







微觀粒子狀態
性質



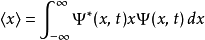











 定態示意圖
定態示意圖









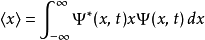










在量子力學裡,定態(stationary state)是一種量子態,定態的機率密度與時間無關。定態是微觀粒子所處狀態中的一種類型的狀態。處於定態的微觀粒子在空間各處出現...
定態與非定態(stationary state and non-stationary state)是指量子力學中微觀體系狀態的兩種不同類型。定態是體系的空間分布和各物理量 取值機率不隨時間改變的...
介紹 定態模擬steady-slate Simulation曾用名穩態模擬,又杯 定態數學模擬。過程對象變數不隨時間變化,模型中不含時 間變數的數學模擬。所謂數學模擬,系利用數學模型...
含有時間變數的稱之為狀態函式,不含時間變數的函式稱之為定態波函式。...... 含有時間變數的稱之為狀態函式,不含時間變數的函式稱之為定態波函式。...
定態假設只能處於一系列不連續的能量狀態中,在這些狀態中,原子中的電子雖然在做變速運動,但並不向外輻射電磁波,這樣相對穩定的狀態稱為定態。...
定態微擾論簡介 編輯 對於大量的實際物理問題,Schrodinger方程能有精確解的情況很少。通常體系的 Hamilton 量是比較複雜的,往往不能精確求解。因此,在處理複雜的實際...
多重定態在通常情況下,對應l確定的外部條件化學反應體系所能達到的定態(即不隨時間變化的狀態)是惟一的。...
弛豫態(relaxing state)系統狀態變數隨時間而變的狀態與定態相反,弛豫態按系統演化規律形成一條演化軌道,對不同初始條件,系統有不同弛豫態演化軌道. ...
當勢函式V不依賴於時間t時,粒子具有確定的能量,粒子的狀態稱為定態。定態時的波函式可寫成式中Ψ(r)稱為定態波函式,滿足定態薛丁格方程,這一方程在數學上稱...
莫爾斯引理(Morse lemma)是關於勢函式在非退化定態點附近定性性質的重要命題。...... 莫爾斯引理(Morse lemma)是關於勢函式在非退化定態點附近定性性質的重要命題。...
波函式定態問題 在量子力學中,一類基本的問題是哈密頓算符不是時間的函式的情況。這時,可以分解成一個只與空間有關的函式和一個只與時間有關的函式乘積,即把它...
