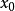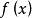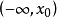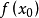莫爾斯引理（Morse lemma）是關於勢函式在非退化定態點附近定性性質的重要命題。
基本介紹
- 中文名：莫爾斯引理
- 外文名：Morse lemma
- 適用範圍：數理科學
簡介,莫爾斯標準型,具體內容,套用,勢函式,
簡介
莫爾斯引理是關於勢函式在非退化定態點附近定性性質的重要命題。
莫爾斯標準型
設f:Rn→R 為一光滑函式，u是它的一個非退化定態點，則在u的某個鄰域U記憶體在一個局域坐標變換Y=(y1,y2,..,y n)，滿足yi(u)=0(i=1,2,...,n)，使得對於一切u∈U，函式f在此局域坐標中變為二次型f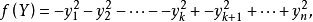
稱為莫爾斯標準型，或莫爾斯k級鞍。式中負項個數k是一個重要參數，稱為非退化定態點的指數。
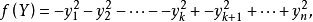
k為拓撲不變數，不因坐標變換而改變。
具體內容
莫爾斯引理保證每個非退化定態點通過一個光滑可逆坐標變換為一個k級莫爾斯鞍點。
k滿足條件0≤k≤n,k=n時勢函式在0點取極大值，k=0時勢函式在0點取極小值，都不是真鞍點。0<k<n時0點才是鞍點。
套用
對於一元勢函式V(X)，引理保證它在莫爾斯點附近與拋物線函式V=±y2有相同的定性性質。
勢函式
勢函式的構造是人工勢場方法中的關鍵問題。勢函式其值為物理上向量勢或是標量勢的數學函式，又稱調和函式，是數學上位勢論的研究主題，同時在平攤分析（amortized analysis）的勢能法中，用來描述過去資源的投入可在後來操作中使用程度的函式。
滿足以下條件的連續函式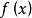
稱為勢函式：
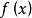
(1)
；
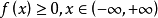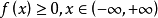
(2)存在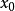
，使得
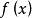在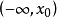
上單調遞增，在
上單調遞減，並稱
為此勢函式的中心點，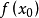
為此勢函式的高度。
