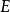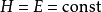重言1形式

在數學中，重言 1-形式（Tautological one-form）是流形 Q 的餘切叢T*Q上一個特殊的 1-形式。這個形式的外導數定義了一個辛形式給出了T*Q的辛流形結構。重言 1-形式在哈密頓力學與拉格朗日力學的形式化中起著重要的作用。重言 1-形式有時也稱為劉維爾 1-形式，典範 1-形式，或者辛勢能。一個類似的對象是切叢上的典範向量場。

基本介紹

• 中文名：重言1形式
• 外文名：Tautological one-form
• 又稱：劉維爾 1-形式，典範 1-形式
• 學科：物理學

詳解

在典範坐標中，重言 1-形式由下式給出：

在差一個全微分（恰當形式）的意義下，相空間中的任何“保持”典範 1-形式結構的坐標系，可以稱之為典範坐標；不同典範坐標之間的變換稱為典範變換。

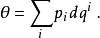
典範辛形式由

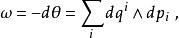
給出。

無坐標定義

重言 1-形式可以相當抽象地定義為相空間上一個 1-形式。設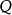 是一個流形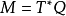， 是其餘切空間或者說相空間。設

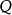
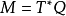
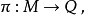
是典範纖維叢投影，令

是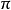誘導的前推。設m是M上一點，然而因為M是餘切叢，我們可將m理解為切空間上一個函式，在

點為：

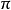
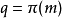
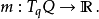
這樣，我們便有m是在q點的纖維中。重言 1-形式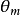在點m定義為

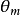
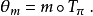
這是一個線性函式

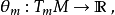
所以

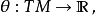
是流形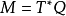上一個 1-形式。不難驗證這種定義和上一節局部坐標的定義是相同的。

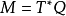
性質

重言 1-形式是惟一“消去”拉回的 1-形式。這便是說：若

是Q上任意一個 1-形式，而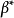 是其拉回。那么

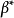
以及

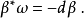
這些都可以用上一節的定義直接得到，如果寫成局部坐標的形式就最好理解：

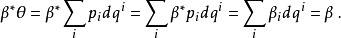
作用量

如果H是餘切叢上一個哈密頓向量場，而 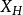是其哈密頓流，那么相應的作用量S為

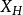
用普通的方式表述，哈密頓流代表了一個力學系統在哈密頓-雅可比方程限制下的軌道。哈密頓流是哈密頓向量場的積分曲線，所以我們用作用量-角度坐標傳統記法：

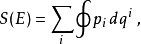
這裡積分理解為在流形上的維持能量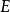為常數 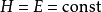的子集上進行。