基本介紹
- 中文名:辛形式
- 外文名:Symplectic vector space
- 領域:數學
簡介
- 斜對稱:ω(u,v) = −ω(v,u),對所有u,v∈V成立;
- 非退化:如果 ω(u,v) = 0 對所有v∈V成立,那么u= 0 。
非退化



- 證明:零向量是唯一的:若a和b為零向量,則 a = a + b = b。
雙線性形式
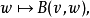

參考
- 多線性映射
- 二次方程式
- 半雙線性形式



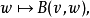

數學中,一個辛矢量空間是帶有辛形式 ω 的向量空間 V,所謂辛形式即一個非退化斜對稱的雙線性形式。...
辛算法的基礎是辛空間、辛變換,類型是矩陣。...... 的基礎,數學,一個辛矢量空間是帶有辛形式ω的向量空間 V,所謂辛形式即一個非退化斜,辛矩陣表示空間的一個辛...
辛幾何(symplectic geometry)與代數幾何和微分幾何是平行的三個數學分支,是研究辛流形(symplectic manifold)的幾何與拓撲性質的學科。它的起源和物理學中的經典力學...
在數學中,重言 1-形式(Tautological one-form)是流形 Q 的餘切叢T*Q上一個特殊的 1-形式。這個形式的外導數定義了一個辛形式給出了T*Q的辛流形結構。重言...
數學中,一個辛向量空間是帶有辛形式ω 的向量空間 V,所謂辛形式即一個非退化斜對稱的雙線性形式。...
數學上,一個辛流形是一個裝備了一個閉、非退化2-形式ω的光滑流形,ω稱為辛形式。辛流形的研究稱為辛拓撲。辛流形作為經典力學和分析力學的抽象表述中的流...
辛空間(symplectic linear space)是一個數學術語,在數學上,辛空間是一類有特殊結構的向量空間。設V是特徵≠2的域K上的向量空間,ω是V上一個反對稱2形式。若ker...
辛識平是新華社《學習進行時》原創品牌欄目“講習所”於2017年3月7日推出的融媒體評論。...
哈密頓系統的的正則方程在辛變換下形式不變,辛算法是基於哈密頓力學的基本原理而提出的保哈密頓系統的差分法,它使離散化後的差分方程保持原有的系統的辛結構。...
辛貝(吲哚布芬片),適應症為動脈硬化引起的缺血性心血管病變、缺血性腦血管病變、靜脈血栓形成。也可用於血液透析時預防血栓形成。...
辛相雄,小說家。日本京都出生。中央大學英文系畢業。1968年在《世代》新人獎中,中篇《希波克拉底的兇相》被選,登上了文壇。以後發表短篇《雙胞胎》、《士兵的休假...
1963年出生,1989年創辦了樂福畜產有限公司。10年來,公司在立足農業、做大產業、扶貧幫困、造福桑梓等方面做出了顯著成績,以“貸兔還毛”的形式,向農戶提供良種兔...
辛設明都要走村串戶,傾聽村民意見,進行調查研究,把農村經濟發展中的困難和問題、農民的呼聲和願望,進行記錄整理,在代表大會會議上以議案和建議的形式傳遞到了省委...
在數學與物理學中,辛向量場(symplectic vector field)是流保持辛形式的向量場。...... 在數學與物理學中,辛向量場(symplectic vector field)是流保持辛形式的向量...
辛伐他汀膠囊,腦卒中 冠心病 高脂血症 高膽固醇血症,湖南正太金琥藥業有限公司生產,處方藥 西藥 膠囊劑...
在數學中,一個辛同胚(symplectomorphism)是辛流形範疇中的一個同構。...... 一個辛向量場的流的積分是一個辛同胚。因為辛同胚保持辛 2-形式,從而也保持辛體積...
一個特定的G-結構(例如,辛形式)上的壯觀的可積性條件可通過擴張程式處理。在這種情形,擴張後的G-結構不能構和線性標架從的一個G-子叢等價。許多情況下,擴張...
從而一個酉結構可以視為一個正交結構、復結構與辛結構,他們要求是“一致的”(意思是說:復結構與辛形式使用同樣的 J,且 J 是正交的;取定一個 J 將所有群...
在數學與物理中,哈密頓向量場是辛流形上一個向量場,定義在任何能量函式或哈密頓函式上。以物理學家和數學家威廉·盧雲·哈密頓命名。哈密頓向量場是經典力學中的...
標準辛空間我們可以展開..Cn。並表示為標準的辛向量空間。確切地說,一個辛形式是一個雙線性形式ω:V×V→R滿足:斜對稱:ω(u, v) = −ω(v, u),對...
不過一般地,只要流形的切叢上有一個處處非退化的雙線性形式(比如辛流形上的辛形式)便可定義這樣的同構。在帶有內積(或更一般的,非退化的雙線性形式)的有限維...
餘切空間有一個標準的辛形式,從中可以一個餘切叢的非退化的體積形式。因此,本身作為一個流形的餘切叢總是可定向的。可以在餘切叢上定義一組特殊的坐標系;這些被...
體積元(volume element)是一種外微分形式,微分流形上與定向相符的外微分形式。更一般地,一個體積元是流形上一個測度。...
