設V是域F上的(n+1)維向量空間,如果函式σ:V×V→F,滿足條件:
σ(ax1+bx2,y)=aσ(x1,y)+bσ(x2,y),a、b∈F,x1、x2、y∈V,
σ(x,ay1+by2)=aσ(x,y1)+bσ(x,y2),a、b∈F,x、y1、y2∈V,
則σ稱為定義在V上的雙線性形式。
基本介紹
- 中文名:雙線性形式
- 外文名:bilinear form
- 所屬學科:數學
- 相關概念:映射、二元映射、共軛線性等
基本介紹

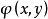
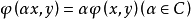
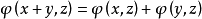
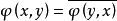
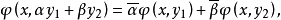
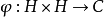
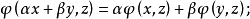

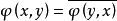
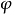
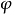
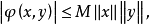
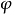
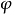
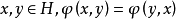
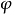
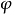
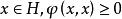
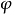
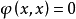
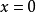
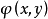
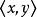

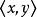
相關定理
定理1
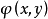
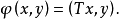
推論
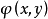
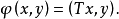
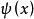
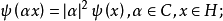
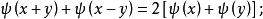
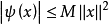
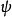
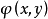
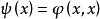
定理2
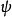

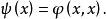
推論
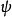
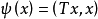
定理3
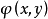

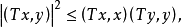

設V是域F上的(n+1)維向量空間,如果函式σ:V×V→F,滿足條件:
σ(ax1+bx2,y)=aσ(x1,y)+bσ(x2,y),a、b∈F,x1、x2、y∈V,
σ(x,ay1+by2)=aσ(x,y1)+bσ(x,y2),a、b∈F,x、y1、y2∈V,
則σ稱為定義在V上的雙線性形式。

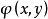
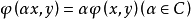
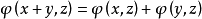
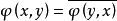
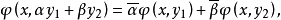
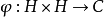
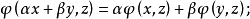

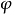
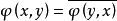
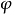
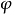
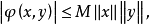
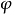
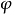
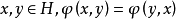
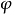
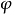
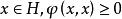
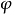
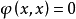
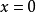
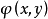
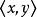

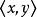
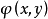
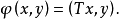
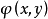
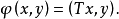
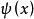
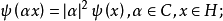
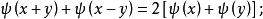
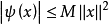
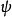
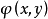
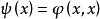
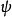

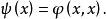
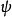
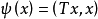
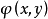

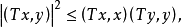
,則稱 為正定的雙線性形式。注: 雙線性形式關於後一個變數實際上是共軛線性的,故而有的書上又稱雙線性形式為一次半線性形式。條件...
在數論中,一個雙線性映射是由兩個向量空間上的元素,生成第三個向量空間上一個元素之函式,並且該函式對每個參數都是線性的。例如矩陣乘法就是一個例子。...
數學中,一個辛矢量空間是帶有辛形式 ω 的向量空間 V,所謂辛形式即一個非退化斜對稱的雙線性形式。...
狄拉克場雙線性型指利用兩個狄拉克場算符和狄拉克矩陣所構造的滿足雙線性的變數。主要有矢量型、贗矢量型、標量型、贗標量型和張量型,與狄拉克矩陣的分類相對應...
,習定義的分段光滑切向量場的集合,則指標形式I(·,·)是定義在.}<a,b)上的對稱雙線性形式方程式介紹其中X,YE.}Ca,b),X'(t)=Dr-X,Y'<t)=Dr.Y.若...
跡形式(trace form)是空間上定義的重要的型。設V是體K上n維線性空間,f是V上關於K的對合J的厄米特型或反厄米特型,ε=±1使f(x,y)=εf(y,x)J (∀...
埃爾米特形式(Hermite Normal form)複流形上的一種特殊雙線性形式。...... 埃爾米特形式(Hermite Normal form)複流形上的一種特殊雙線性形式。中文名 埃爾米特形式...
4維流形相交形式(the intersection formon 4-manifolds)定義在緊緻單連通4維流形上的雙線性形式,用它可以確定4維流形的同倫型與分類性質.設M為緊緻單連通的4...
2.8.4 雙線性形式證明(n=2和n=3)第三章 線性波動方程3.1 線性波動方程的經典解3.2 線性波動方程的弱解3.3 能量不等式3.4 線性波動方程解的存在與唯一性...
在低層的域的特徵不是2的時候,二次形式等價於對稱雙線性形式。二次形式總是生成對稱雙線性形式(通過極化恆等式),而反過來要求除以2。...
和它的相伴雙線性形式 有同樣的核。雙線性形式 被稱為非奇異的,如果它的核是0;二次形式Q被稱為非奇異的,如果它的核是0。非奇異二次形式 的正交群是保持二...
對一般任何域上的有限維向量空間上的雙線性形式B,我們可對一組向量 定義一個格拉姆矩陣G為 。如果雙線性形式B對稱則該格拉姆矩陣對稱。...
因為每個正定形式都是非退化的,黎曼度量是偽黎曼度量的一個特殊例子。固此,可以把黎曼流形歸納為偽黎曼流形。每一個非退化對稱,雙線性形式有一個固定的度量符號 ...
定義一個格拉姆矩陣 G為 。如果雙線性形式 B對稱則該格拉姆矩陣對稱。GRAM性質 編輯 1.半正定格拉姆矩陣是半正定的,反之每個半正定矩陣是某些向量的格拉姆矩陣。這...
線性運算元第一個內插定理是M.Rierz在1926年作為雙線性形式的不等式得出的。線性運算元內插法與內插空間理論是泛函分析學科的一個新的研究領域,它的生命力不僅表現在...
在雙線性代數中,正定矩陣的性質類似複數中的正實數。與正定矩陣相對應的線性運算元是對稱正定雙線性形式(復域中則對應埃爾米特正定雙線性形式)。 中文名 正定矩陣 ...
酉群Un(R) 是保持某個模的半雙線性形式的群。有子群特殊酉群SUn(R),以及他們的商群射影酉群PUn(R) =Un(R)/Z(Un(R)) 與射影特殊酉群PSUn(R) =...
在一個向量空間V中,定義在 上的正定對稱雙線性形式函式即是V的數量積,而添加有一個數量積的向量空間即是內積空間。點積代數定義 設二維空間內有兩個向量 和 ,...
嘉當-迪奧多內定理是數學中以埃利·嘉當與讓·迪厄多內命名的定理,此定理所涉及的是對稱雙線性形式的自同構群。...
在雙線性代數中,正定矩陣的性質類似複數中的正實數。與正定矩陣相對應的線性運算元是對稱正定雙線性形式(復域中則對應埃爾米特正定雙線性形式)。...
拓撲4維流形弗里德曼定理(Freedman the-orem on topological 4-manifolds)是闡明4維流形的拓撲分類與相交形式之間關係的一個定理。根據關於對稱雙線性形式的分類與...
設V是m維向量空間,在V上定義了一個反對稱、非退化的雙線性形式σ,即σ滿足:①反對稱性,σ(α,β)=-σ(β,α),對任意α,β∈V成立;②非退化,若對任意...
不過一般地,只要流形的切叢上有一個處處非退化的雙線性形式(比如辛流形上的辛形式)便可定義這樣的同構。在帶有內積(或更一般的,非退化的雙線性形式)的有限維...
