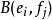雙線性映射

在數論中，一個雙線性映射是由兩個向量空間上的元素，生成第三個向量空間上一個元素之函式，並且該函式對每個參數都是線性的。例如矩陣乘法就是一個例子。

基本介紹

• 中文名：雙線性映射
• 外文名：bilinear mapping
• 例子：矩陣乘法
• 套用學科：數學
• 屬於：函式
• 相關術語：線性映射

定義

設V,W和X是在同一個基礎域F上的三個向量空間。雙線性映射是函式。

• B:V×W→X
  

使得對於任何W中w，映射

• v↦B(v,w )
  

是從V到X的線性映射，並且對於任何V中的v，映射

• w↦B(v,w )
  

是從W到X的線性映射。

換句話說，如果保持雙線性映射的第一個參數固定，並留下第二個參數可變，結果的是線性運算元，如果保持第二個參數固定也是類似的。

如果V=W並且有B(v,w ) =B(w,v )對於所有V中的v,w，則我們稱B是對稱的。

當這裡的X是F的時候，我們稱之為雙線性形式，它特別有用(參見例子標量積、內積和二次形式)。

如果使用在交換環R上的模替代向量空間，定義不需要任何改變。還可容易的推廣到n元函式，這裡正確的術語是“多線性”。

對非交換基礎環R和右模M_R與左模_RN的情況，我們可以定義雙線性映射B:M×N→T，這裡的T是阿貝爾環，使得對於任何N中的n，m↦B(m,n )是群同態，而對於任何M中的m，n↦B(m,n )是群同態，並還滿足

• B(mt,n ) =B(m,tn )
  

對於所有的M中的m，N中n和R中的t。

性質

定義的V,W,X是有限維的，則L(V,W;X)也是。對於X=F就是雙線性形式，這個空間的維度是dimV×dimW（儘管線性形式的空間L(V×W;K)的維度是dimV+dimW）。要看出來，選擇V和W的基；接著每個線性映射可以唯一的表示為矩陣{\displaystyle B(e_{i},f_{j})}，反之亦然。現在，如果X是更高維的空間，我們明顯的有dimL(V如果V,W,X是有限維的，則L(V,W;X)也是。對於X=F就是雙線性形式，這個空間的維度是dimV×dimW（儘管線性形式的空間L(V×W;K)的維度是dimV+dimW）。要看出來，選擇V和W的基；接著每個線性映射可以唯一的表示為矩陣 ，反之亦然。現在，如果X是更高維的空間，我們明顯的有dimL(V,W;X)=dimV×dimW×dimX。

例子

• 矩陣乘法是雙線性映射M(m,n)×M(n,p) → M(m,p)。
  
• 如果在實數R上的向量空間V承載了內積，則內積是雙線性映射V×V→R。
  
• 一般的說，對於在域F上的向量空間V，在V上的雙線性形式同於雙線性映射V×V→F。
  
• 如果V是有對偶空間V*的向量空間，則套用運算元b(f,v) =f(v)是從V*×V到基礎域的雙線性映射。
  
• 設V和W是在同一個基礎域F上的向量空間。如果f是V* 的成員而g是W* 的成員，則b(v,w) =f(v)g(w)定義雙線性映射V×W→F。
  
• 在R中叉積是雙線性映射R×R→R。
  
• 設B:V×W→X是雙線性映射，而L:U→W是線性運算元，則(v,u) →B(v,Lu)是在V×U上的雙線性映射。
  
• 零映射，定義於B(v,w)=o對於所有V×W中的(v,w)，是從V×W到X的同時為雙線性映射和線性映射的唯一映射。實際上，如果(v,w)∈V×W，則 B(v,w)=B(v,o)+B(o,w)=o+o。