雙線性型是數學術語。設 f 是線性空間 V 上的雙線性函式,如果它在某組基下的度量矩陣 A 是可逆矩陣,則稱 f 是非退化的雙線性函式,否則稱為退化的雙線性函式。
基本介紹
- 中文名:雙線性型
- 外文名:bilinear form
- 別名:雙線性函式或雙線性映射
- 公式:ψ(x,b1y1+b2y2)=b1
- 類型:數學名詞
定義
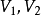

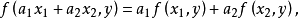
性質
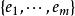
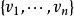
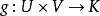

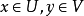
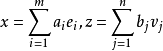
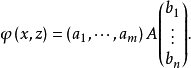
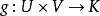
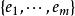
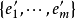
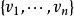

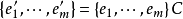
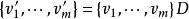
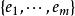
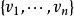
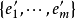

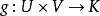
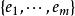
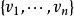
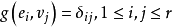
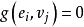

雙線性型是數學術語。設 f 是線性空間 V 上的雙線性函式,如果它在某組基下的度量矩陣 A 是可逆矩陣,則稱 f 是非退化的雙線性函式,否則稱為退化的雙線性函式。
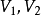

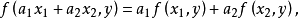
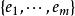
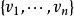
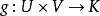

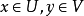
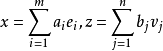
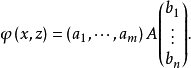
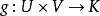
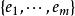
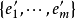
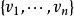

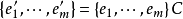
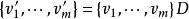
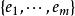
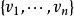
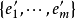

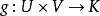
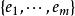
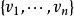
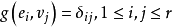
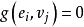
雙線性型是數學術語。設 f 是線性空間 V 上的雙線性函式,如果它在某組基下的度量矩陣 A 是可逆矩陣,則稱 f 是非退化的雙線性函式,否則稱為退化的雙線性...
強迫雙線性型(coercive bilinear form)用泛 函分析方法研究橢圓邊值問題需要的一種重要的雙 線性型.設V是復(實)希爾伯特空間,a(u,v)是V 上的雙線性型,即對...
對稱雙線性型(symmetric bilinear form)是線性空間V上的雙線性型f(α,β),如滿足:對所有α,β∈V,都有f(α,β)=f(β,α),則稱f(α,β)為對稱雙線性...
,則稱 為正定的雙線性形式。注: 雙線性形式關於後一個變數實際上是共軛線性的,故而有的書上又稱雙線性形式為一次半線性形式。條件...
雙線性函式(bilinear function )是線性函式的推廣。設V1,V2是域P上的線性空間,V1×V2到P的雙線性映射φ稱為V1×V2上的雙線性函式。特別地,當V1=V2=V時,...
狄拉克場雙線性型指利用兩個狄拉克場算符和狄拉克矩陣所構造的滿足雙線性的變數。主要有矢量型、贗矢量型、標量型、贗標量型和張量型,與狄拉克矩陣的分類相對應...
當f是交錯雙線性型時Un(K,f)就是辛群Spn(K,f);當K的特徵≠2且f是對稱雙線性型時Un(K,f)就是正交群On(K,f);當K是複數域,J是復共軛,H=I時,酉群...
當f是交錯雙線性型時Un(K,f)就是辛群Spn(K,f);當K的特徵≠2且f是對稱雙線性型時Un(K,f)就是正交群On(K,f);當K是複數域,J是復共軛,H=I時,酉群...
當f是交錯雙線性型時Un(K,f)就是辛群Spn(K,f);當K的特徵≠2且f是對稱雙線性型時Un(K,f)就是正交群On(K,f);當K是複數域,J是復共軛,H=I時,酉群...
設V是實數域R上的線性空間(或稱為向量空間),若V上定義著正定對稱雙線性型g(g稱為內積),則V稱為(對於g的)內積空間或歐幾里德空間(有時僅當V是有限維時,...
正交幾何(orthogonal geometry)是一種向量空間的幾何,即關於非退化對稱雙線性型的向量空間的研究。這裡的對稱雙線性型B是指對任意向量x,y有B(x,y)=B(y,x)的...
拉克斯一密格拉蒙定理(Lax-Milgram theorem) 用來證明線性橢圓方程邊值問題有解的一個重要定 理.該定理斷言:如果a(u,v)是希爾伯特空間V上 的連續強迫雙線性型,...
主要內容包括:整數和多項式,線性方程組,線性映射,矩陣和行列式,線性空間和線性映射,線性變換,歐幾里得空間,線性型,雙線性型以及二次型。《Linear Algebra》適合數學系...
定義一個對稱雙線性型 k:g×g→F;對於X、Y∈g, 定義k(X,Y)=Trρ(X)·ρ(Y)(ρ(X)ρ(Y)的跡)。特別,當g是有限維的而ρ是伴隨表示ad時, k稱為...
《高等代數學》主要內容為線性代數,包括數與多項式,行列式,線性方程組,矩陣,線性空間,二次型,線性變換,空間分解,矩陣相似,歐空間和酉空間,雙線性型;選學內容有...
