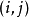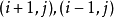格線自動生成

格線生成，是把一個特定的研究區域分割成由許多很小的子區域(元素)，以滿足一些特定的要求。在理想的情況下，格線中的每個元素的形狀和分布可以通過一種自動的格線生成算法來確定。

目前為止，根據格線的連線關係來區分，主要有兩大類結構化格線和非結構化格線。結構化格線生成算法主要有無限插值方法和偏微分方程格線生成方法；非結構化格線生成算法主要有結點連元法、映射法和Delaunay 三角化方法。

基本介紹

• 中文名：格線自動生成
• 外文名：Automatic mesh generation
• 格線分為：非結構化格線；結構化格線
• 常用方法：無限插值方法；偏微分方程格線等
• 相關：有限元方法
• 領域：自動控制

背景

在連續的物理系統中，如在飛機周圍的氣流，水壩上水對水壩的集中壓力，積體電路中電子的電場，或是在化學反應中的反應物的濃度等，都是需要套用偏微分方程來模擬的。想要在計算機上模擬這些系統，這些連續的方程需要首先離散化，結果產生一組由有限個離散點組成的空間或平面包括對應的時間序列，在這些點上，我們才可以分別對所要研究的變數，如電壓，密度，和電場等進行計算。離散化的通常方法有有限差分，有限體積和有限元方法，這些方法通過相鄰的點來計算出變數的導數。這些計算需要基於一定的格線來實現，所以格線的概念也就隨之產生。

隨著格線套用的不斷廣泛和深入，人們就自然而然產生了一種動機，要去實現和改進自動化格線生成算法。在起初的時候，套用有限元方法的人們用幾十或是幾百個格線單元來模擬一個很大的簡化了的規則區域，他們己經感到很滿意了。要把一塊區域人工的劃分成一系列有用的格線單元，這樣的預處理工作非常的艱辛。而現在人們只需要點一下按鈕，就可以通過軟體來輕鬆的自動生成複雜的格線，這些格線包含了成千上萬的格線單元，而不需要任何繁瑣的預處理工作。

分類

目前為止，根據格線的連線關係來區分，主要有兩大類結構化格線和非結構化格線。

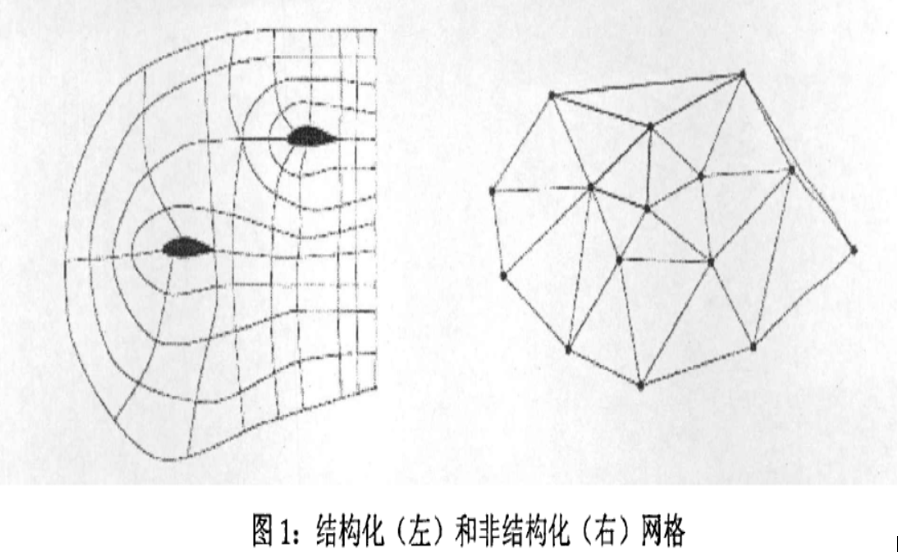
結構化格線主要是指對每一個格線節點，其對鄰接的其他節點的連線數是一定的或有規則的對一些格線，可能會有一線部分節點與其他節點的連線數是不同的。

非結構化格線是指的每一個格線節電與其他節點的連線關係是不確定的或不規則的。

圖1給出了一個著兩種不同形式的格線的一個簡單例子。在有些情況下，整個格線的一部分可以是結構化的，而另一部分又是非結構化的譬如在河道流域中，邊界上的格線是結構化的而流域內部是非結構化的。

結構化格線生成

邊界固定型的格線

所謂結構化格線是指，它的格線所有節點的連線關係是規則的。例如，格線中的所有格線點能夠通過索引方便的查找和確定(在二維中通過兩個索引確定，三維中則是三個索引)。每個格線點的鄰接點能夠方便的同過索引計算出來，而不是去一一查找（例如，格線點 的鄰接點就是 等等）。在規則的矩形區域上的格線生成雖然簡單，但其價值不大，規則的格線生成技術主要專注於對不規則的邊界區域進行格線化，例如，血管中血的流向，或者血管得變形，金屬中熱量的傳導等等。通常格線的生成必須符合它的邊界，用某一面坐標來形成（部分）格線邊界。這種方法在邊界處可以提供精確的結果，速度也很快。對於流體研究中，這種格線可以作為波動模型的很好套用，因為流體研究中往往需要格線要和區域的邊界很好的吻合起來。另外一種選擇便是套用一個簡單的矩形格線作為基礎，在區域的邊界處通過格線裁剪，使其符合邊界的要求，然後對那些邊界上不夠理想的格線再用局部的修飾，從而得到我們的最終結果（笛卡爾格線）。這種方法在區域的邊界處打斷了格線的順序，還要刪除一些格線單元，這些都增加了格線生成算法的複雜度。迪卡爾格線的生成速度是很快的，在空氣動力學中套用較多。但似乎不適用於 Navier-Stokes空氣動力學。

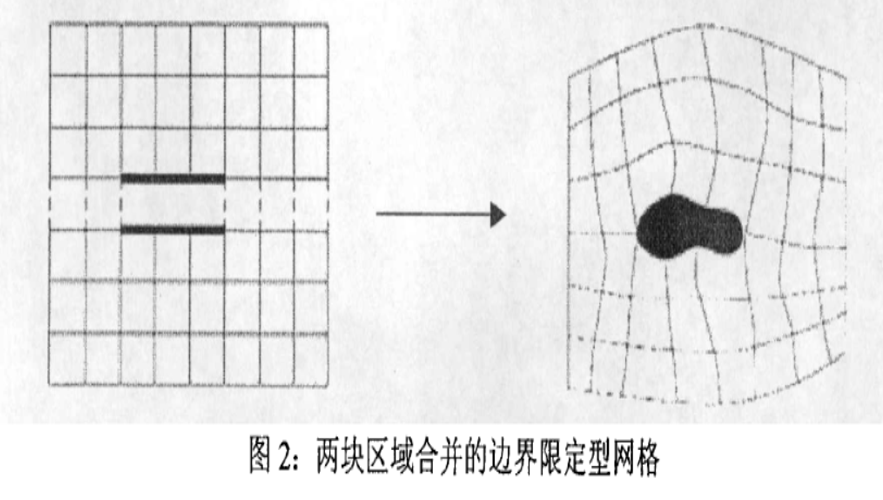
生成區域邊界固定格線的最常用方法是需要產生一個連續的，並在邊界上完全符合的格線。也就是要找到一種方法，把一組連續毗鄰的矩形可計算區域通過曲線邊界映射到一個實際的物理區域如圖2。

如果希望不添加任何額外不規則的偏斜格線，又能用一個映射關係把一個規則的矩形可計算格線映射到一個複雜的區域上，這幾乎是非常困難的。為了要繞開這個問題，要把區域分成羅幹個子區域，對每個區域再進行格線劃分。在子區域與子區域的結合處，格線的連線必須要連續的。這就是多分塊格線的主要思想。對於區域的分解，一般都通過工具手工完成，雖然這比較慢。

另外一種用多化分塊思想來生成連續的邊界擬合格線的方法是，在邊界區域上，我們用固定邊界的格線生成法，在區域的內部用規則的矩形格線，在兩種格線較叉的區域，我們通過插值方法來使格線點相匹配。這樣生成的格線叫Chimera格線。

Chimera格線對於移動的邊界（例如，在直升機機翼葉片中）或多條邊界混合（流動中的粒子）非常有用。因為這樣格線的絕大部分格線單元始終都是固定的，而只有邊界上通過插值的格線單元是隨著邊界的變化而變化的。Chimera格線卻是有其獨特的優點，最近守恆插值方法的發展又增加了它的有甩性。但是，一大批的結構化格線生成方法都是基於區域分塊化思想，故下面主要是討論這一思想方法的套用。

無限插值方法（TFI）

1973年Gardon 和 Hall 在多變數概念的基礎上提出了生成格線的無限插值理論，缺點是不易控制物面附近的格線趨勢。 1981年Eriksson 與 Rizzi 提出改進的無限插值理論思想，即在文獻的基礎上引進物面笛卡兒坐標變數關於物面逸出變數的導數，利用這些導數來控制物面附近的格線變換。

用這種理論構造格線時，需要：

1）定義邊界上的格線分布

2）在物面上 構造上述導數

3）構造插值時需用的型函式

其中，2）是困難且關鍵的步驟。

偏微分方程格線生成(PDE)

PDE方法可分為橢圓型 、拋物型及雙曲型 3 種。

70 年代初，自 Thompson等人首先提出了求解偏微分方程生成貼體格線方法，並首次套用於二維物體繞流的數值計算以來，該方法已成為生成複雜幾何外形貼體格線的主要技術。通過數值求解橢圓型方程生成曲線坐標系，由於橢圓型方程固有的可以光順邊界數據的特性，即抑制所求邊界當地的不連續性向場內部的傳遞，從而使其成為一種非常有效的數值格線生成方法。採用求解橢圓型方程組技術，進 一步調整內部及邊界格線的疏密分布和正交性，以滿足黏流數值模擬和插值精度的需要。

非結構化格線生成

非結構化格線主要是為了有限元方法的套用而發展起來的。對於有限元方法，可以有很多適用於計算的單元體四面體單元、稜柱體單元、塊狀體單元，它們之間的連線關係是不定的，這種特性也就是非結構化格線的本質。但是，其中能夠完全的通過自動化過程來生成格線的單元只有三角形二維空間、和四面體三維空間。雖然方塊單元是理想的，但對於方塊單元要想完全自動化生成格線是很困難的必須在區域的某些地方加入稜柱體或四面體來補充。

映射法

映射法出現於 20 世紀 70 年代，是最早採用的格線生成方法。從 70 年代開始套用於商品化系統中，比如 FEM GEN。目前映射法在現有的商品化系統中仍占統治地位，它是根據形體邊界的參數方程，利用適當的映射函式，將待分區域映射到參數空間中形成規則參數域，對規則參數域進行格線剖分，將參數域的格線 (二維是正方形 ，三維是立方體) 反向映射回歐氏空間，從而生成實際的格線。

映射法可分為三大類 :保角映射法、基於偏微分方程法、代數插值法。

三維格線劃分的許多方法都是先將形體的表面離散化，所以曲面映射是三維映射的基礎。在空間參數曲面格線的生成中，根據曲面邊界的性質有單線性映射、雙線性映射 、三線性映射。

映射法的優點是：計算效率高，格線分布均勻、排列整齊，便於直接生成四邊形、六面體等高精度單元。但是，映射法對於形狀較為複雜的形體適應性差，需要將複雜形體事先分解成若干形狀簡單的子域。子域分解繁瑣費時，人工互動多，難以實現全自動化。

結點連元法

結點連元法形成格線的過程是先布點，後將結點連線生成單元。隨機布點法不能保證布點均勻，且點距檢查計算耗時效率低；直接布點法中，長方形格線直接布點法和等距水平線掃描法雖然方法簡單、算法快速、布點比較均勻，但單一死板，不能避免產生最後剩餘的空白地帶；硬幣填充法布點均勻，能較好地避免產生最後剩餘的空白地帶。總的來講，結點連元法的優點是：對於複雜形體適應能力強，與其他方法相比能容易實現格線生成的自動化，所以也有人將該方法直接叫做自動化格線劃分方法，此外，該方法生成的單元形狀良好；缺點是計算量大、效率低。

Delaunay三角化方法

這種方法實質上也是結點連元法。Delaunay三角劃分在散亂數據場的可視化 、逆向工程 、地理信息系統 (如地貌的不規則格線建模) 、VRML 產品建模等領域都有十分廣泛的套用，尤其在有限元格線自動生成方面廣為流行。

在平面域的 Delaunay 三角劃分中，理論上已經嚴格證明，只要給定的結點分布中不存在四點及四點以上共圓時，有最優解，即所有三角形單元中最小內角之和可達到最大值。在 Delaunay 三角劃分後，形成許許多多彼此相連的 Voronoi 多邊形，每個只有一個結點，每一個 Voronoi 多邊形的邊實際上就是其內結點與相臨 Voronoi 多 邊形內結點連線的中垂線，所有Voronoi 多邊形的集合叫做 Dirichlet 圖，連線相臨Voronoi 多邊形內的結點便形成三角形格線。

實現Delaunay 三角剖分的方法很多，常用的一種算法是逐個插入結點的遞歸算法。該算法要求生成Delaunay 三角形的外接圓內不允許存在其他結點，若有其他結點，則應局部修改原來的剖分。基本過程為：先構造一個大外接圓，將所有結點都包含進去，然後找出已有三角形中哪些三角形的外接圓內包含新加入的結點，刪除這些三角形內離新結點距離最近的一條邊，將新結點與周圍的老結點連線形成新的三角剖分。